Предмет: Математика,
автор: sejpakvlad
ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ 4.24
Приложения:
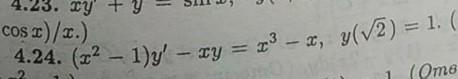
Ответы
Автор ответа:
1
Ответ:
Это линейное ДУ.
общее решение
частное решение
Похожие вопросы
Предмет: Русский язык,
автор: alexan62
Предмет: Русский язык,
автор: Stan123
Предмет: Русский язык,
автор: cgfcgfvhgfex
Предмет: Математика,
автор: TlTOV
Предмет: Окружающий мир,
автор: Jonica07