Предмет: Алгебра,
автор: darvin2354
Неравенство (x-a)(3x+2)(x+b)>0 имеет решение (-7;-2/3) U (5;&)
(Сделайте хотя бы одно из двух пожалуйста )
Приложения:
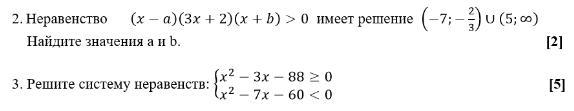
Ответы
Автор ответа:
3
Ответ:
darvin2354:
помоги пожалуйста сделать это умоляю https://znanija.com/task/44849021?answeringSource=feedPublic%2FhomePage%2F29
Похожие вопросы
Предмет: Русский язык,
автор: anna19762004
Предмет: Русский язык,
автор: vershininanata
Предмет: Русский язык,
автор: cgfcgfvhgfex
Предмет: Математика,
автор: olyakurets
Предмет: Русский язык,
автор: DanilKos2018