49 БАЛЛОВ. Решить задачу с параллелограммом

Ответы
Ответ:
(см. объяснение)
Пошаговое объяснение:
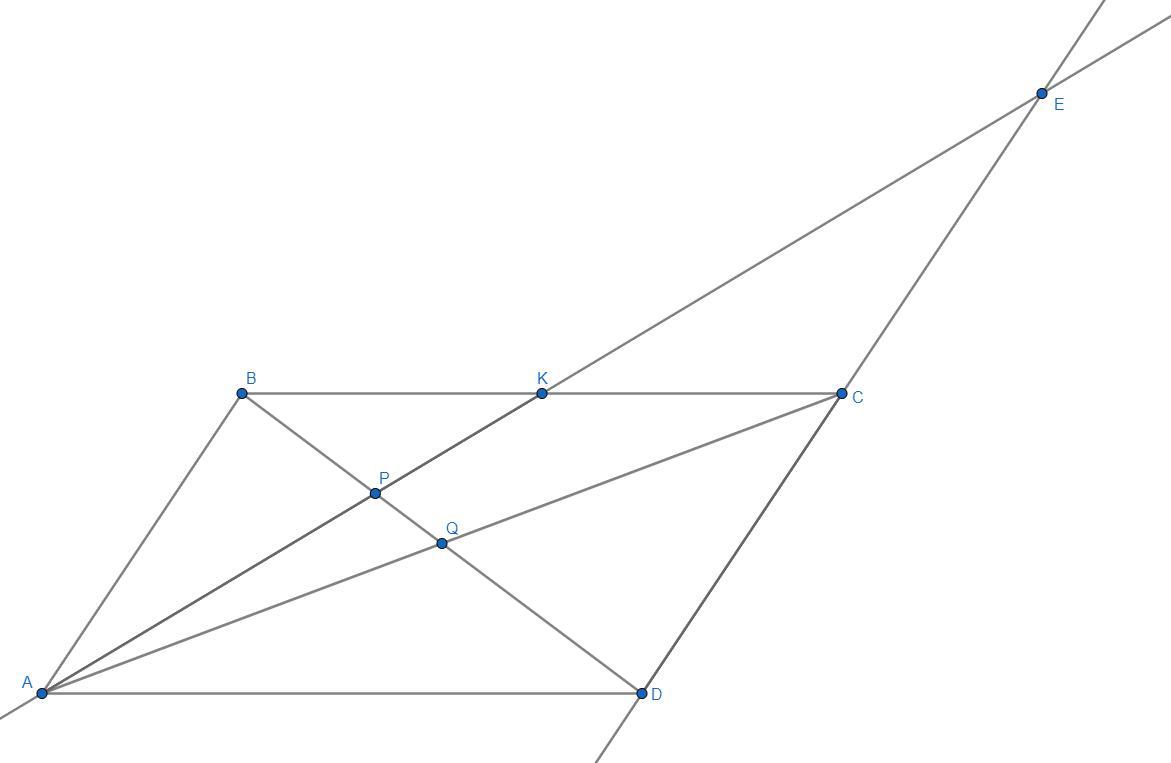
Продлим AK до пересечения с прямой DC. Пусть точка пересечения будет иметь имя E. Т.к. KC равна половине AD и KC||AD, то KC - это средняя линия треугольника AED. Тогда DE=2DC=2AB. Треугольники ABP и DPE подобны с коэффициентом подобия . Тогда их площади относятся, как
, т.е.
. Теперь заметим, что по второму признаку равенства треугольников ΔABK=ΔECK. Тогда
, где S - площадь исходного параллелограмма ABCD. Обратим теперь внимание, что
. Но
. Значит
. Подставляя в равенство выше, имеем, что
. Не забывая, что
, приходим к тому, что
. Теперь проделаем похожую работу для
. Для этого выполним преобразования:
. Теперь вернемся к тому, что
.
Так мы получили, что .
Задача решена!
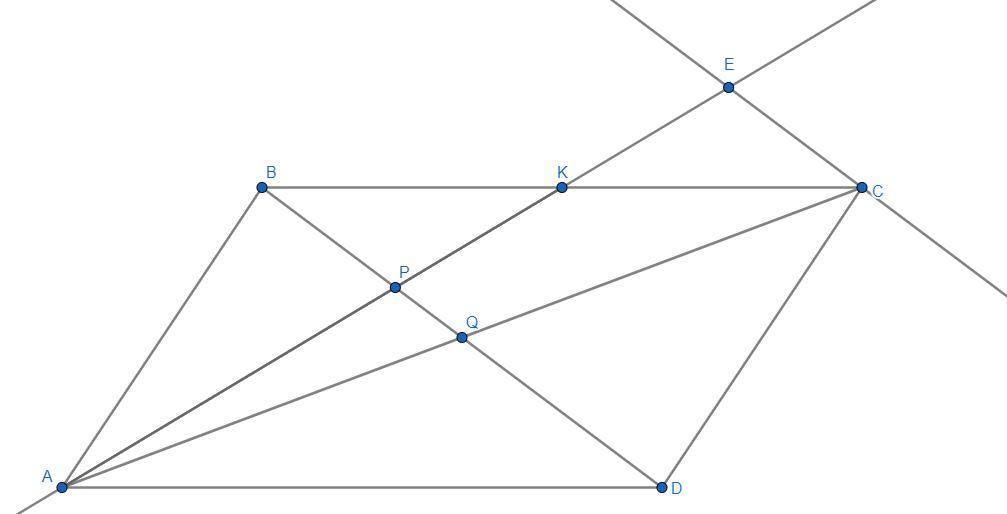
Приведу другой способ решения:
Пусть пересечение AK и прямой, проходящей через точку C параллельной BD, будет называться точкой E. Тогда, рассмотрев подобие треугольников AEC и APQ, а также, увидев, что ΔKEC=ΔKBP, можно, применив аналогичный решению выше подход, за более короткое число преобразований прийти к верному ответу. Требуемое дополнительное построение показано в прикрепленном к решению рисунке. Такой способ, пожалуй, даже лучше приведенного выше.