Предмет: Математика,
автор: niky21
Основание пирамиды - ромб со стороной 12 см и углом 60 °. определенный
объем пирамиды, если двугранные углы у основания пирамиды равны 30 °
Ответы
Автор ответа:
0
Ответ:
72√3см³
Пошаговое объяснение:
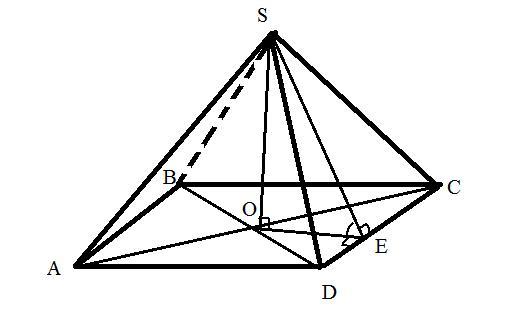
Пусть SABCD - пирамида, в которой двугранные углы у основания равны. Тогда SO - высота пирамиды, вершина S проецируется в центр вписанной окружности в ромб ABCD при основании. <BAD=60°
S(осн)=АВ²*sinBAD=144*√3/2=72√3см²
ОЕ - радиус вписанной окружности может быть найден по формуле
r=S/p, где S=S(осн), а р - полупериметр ромба, р=2*АВ=2*12=24
ОЕ=72√3/24=3√3см
Двугранный угол пирамиды при основании равен 30°, значит линейный угол <SEO=30°.
В прямоугольном треугольнике SOE:
tgSEO=SO/OE
SO=OE*tgSEO=3√3*tg30°=3√3/√3=3см
V=1/3*S(осн)*SO=1/3*72√3*3=72√3см³
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 1Ленчик1
Предмет: Английский язык,
автор: Samsonya2015
Предмет: Математика,
автор: kaechludmila
Предмет: Математика,
автор: S1mpleBELKA