Предмет: Математика,
автор: artpyl2
70 БАЛЛОВ. Упростите тригонометрическое выражение.
Приложения:
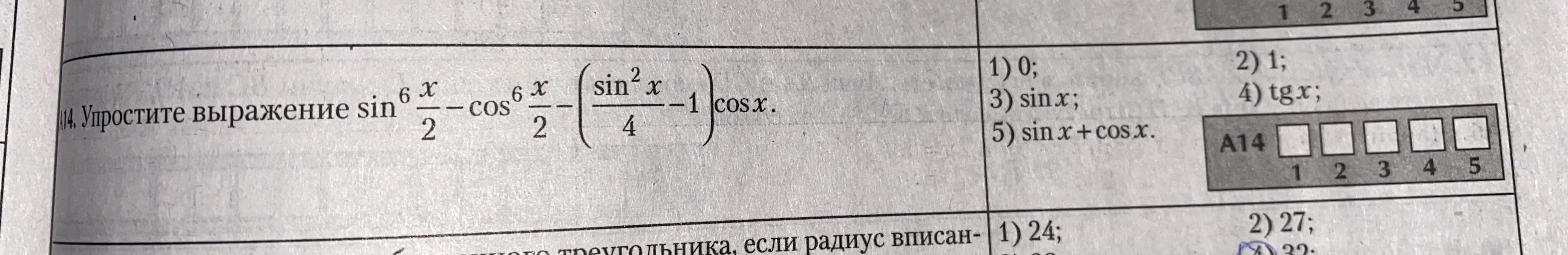
Ответы
Автор ответа:
1
Для первой разности используем формулу разности кубов, косинуса двойного аргумента, квадрата суммы и синуса двойного аргумента:
В результате разность двух одинаковых выражений равна нулю.
Ответ: 0.
Похожие вопросы
Предмет: Русский язык,
автор: bigima
Предмет: Русский язык,
автор: sborov1
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: darsmolkina
Предмет: Русский язык,
автор: varya22011