Комплексные числа
Найти:
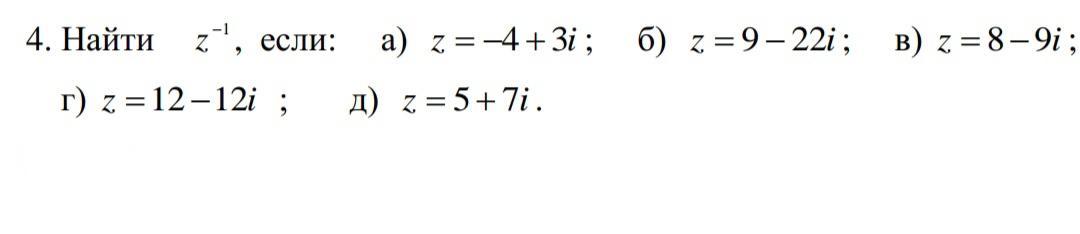
Ответы
а) 1/z = 1/(-4+3i) = (-4-3i)/((-4-3i)·(-4+3i)) = (-4-3i)/(4²- (3i)²) = (-4-3i)/(16+9) =
(-4-3i)/25 = - 4/25 - i·3/25 = -0,16 - i·0,12. (i² = - 1 - по определению)
б) 1/(9-22i) = (9+22i)/((9-22i)(9+22i)) = (9+22i)/(9²+22²) = (9+22i)/565 =
9/565 + i·22/565
в) 1/(8-9i) = (8+9i)/((8-9i)(8+9i)) = (8+9i)/(64+81) = (8+9i)/145 = 8/145 + i·9/145
г) 1/(12-12i) = (1+i)/(12(1-i)(1+i)) = (1+i)/(12·(1+1)) = (1+i)/24 = 1/24 + i/24
д) 1/(5+7i) = (5-7i)/((5+7i)(5-7i)) = (5-7i)/(25+49) = (5-7i)/74 = 5/74 - i·7/74
Во всех случаях 1/z сводилась к алгебраическому представлению комплексного числа: a + ib. Для избавления дроби от комплексного знаменателя применялся метод домножения на комплексно сопряженное: x-iy будет сопряженным x+iy, к тому же (x-iy)·(x+iy) = x² + y²