Предмет: Алгебра, автор: sse1r

Комплексные числа

Вычислить

Приложения:

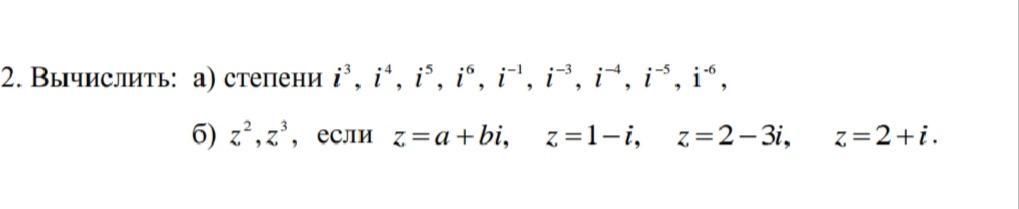
amanda2sempl: i= exp(iп/2), i^3 = exp(i3п/2) = сos(3п/2)+i*sin(3п/2) = - i, i^4 = (-1)^2 = 1

amanda2sempl: i^5 = i * i^4 = i, i^6 = i^2 * i^4 = -1*1 = -1

amanda2sempl: i ^ (-1) = 1/i = i / (i*i) = -i, i^(-3) = i/(i^4) = i/1 = i, i^(-4) = 1/(i^4) = 1

amanda2sempl: i^(-5) = i^(-1) * i^(-4) = - i, i^(-6) = i^(-2) * i^(-4) = -1 * 1 = -1

amanda2sempl: (1-i)^2 = 1 - 2i + i^2 = 1 - 2i - 1 = -2i, (1-i)^3 = (1-i) * (1-i)^2 = (1-i)(-2i) = -2i + 2i*i = -2-2i

amanda2sempl: (2-3i)^2 = 4 - 12i + 9i*i = 4 -12i - 9 = -5 - 12i, (2-3i)^3 = (2-3i)*(2-3i)^2 = (2-3i)(-5-12i) = -10 - 24i + 15i + 36i*i = -10 - 9i - 36 = - 46 - 9i

amanda2sempl: (2+i)^2 = 4 + 4i - 1 = 3 + 4i, (2+i)^3 = 2+i) * 2+i)^2

amanda2sempl: (2+i)^3 = (2+i) *( 2+i)^2 = (2+i)* (3 + 4i) = 6 + 8i + 3i - 4 = 2 + 11i

amanda2sempl: (a + ib)^2 = a^2 - b^2 + 2aib, (a + ib)^3 = (a + ib) * (a + ib)^2 = (a + ib)*(a^2 - b^2 + 2aib) = a^3 - ab^2 + 2iba^2 + iba^2 - ib^3 - 2ab^2 = a^3 - 3ab^2 + i(3ba^2 - b^3) = a(a^2 - 3b^2) + ib(3a^2 - b^2)

sse1r: Спасибо огромное