Предмет: Математика,
автор: sadovyi876
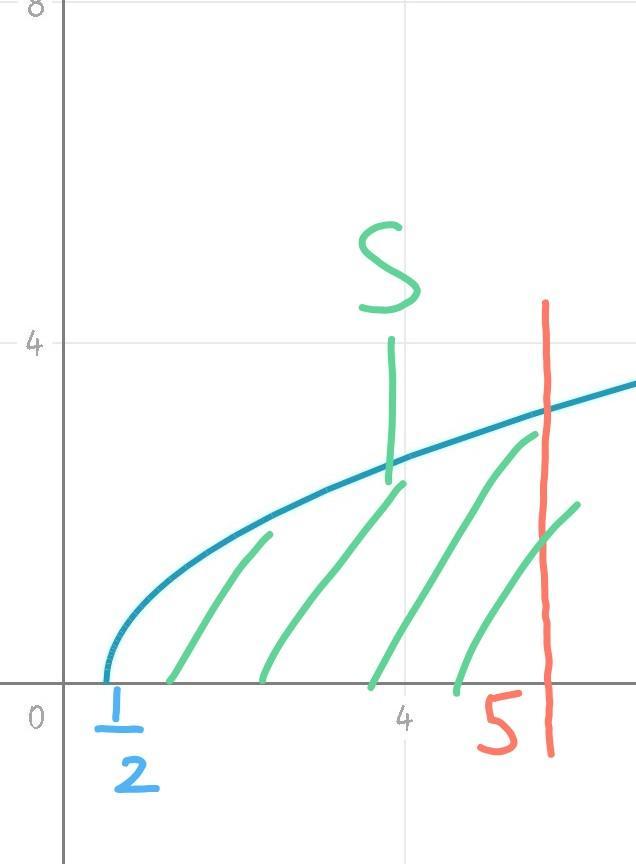
Обчисліть площу фігури, обмежуної лініями y= , y=0 , x=5
, y=0 , x=5
Ответы
Автор ответа:
0
Пересечение с ОХ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: margoelza
Предмет: Английский язык,
автор: LenaSad
Предмет: Окружающий мир,
автор: Alisa20060408
Предмет: Английский язык,
автор: Аноним