Предмет: Математика,
автор: babymama17
помогите пожалуйста решить 13 номер из ЕГЭ по математике (профиль)
Приложения:
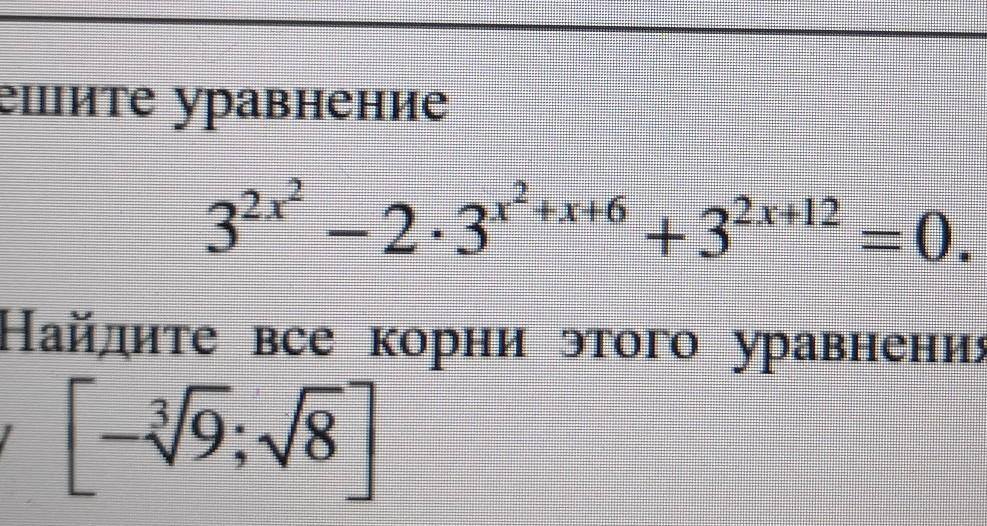
coolunnameduser:
Тут к виду (a+b)^2 свести можно
каким образом?
(3^x²)²-2*3^x²*3^{x+6} + 3^{x+6}² = 0
(3^x² - 3^{x+6})^2 = 0
Ответы
Автор ответа:
1
3^2x² - 2*3^(x² + x + 6) + 3^(2x + 12) = 0 |: 3^(x² + x + 6)
3^(x² + x + 6) ≠ 0
3^2x²/3^(x² + x + 6) = 3^(2x² - x² - x - 6) = 3^(x² - x - 6)
3^(2x + 12)/ 3^(x² + x + 6) = 3^(2x + 12 - x² - x - 6) = 3^(- x² + x + 6)
3^(x² - x - 6) - 2 + 3^(-x² + x + 6) = 0
3^(x² - x - 6) = t
3^(-x² + x + 6) = 1/t
t - 2 + 1/t = 0
(t² - 2t + 1)/t = 0 |*t
(t - 1)² = 0
t = 1
3^(x² - x - 6) = 1
x² - x - 6 = 0
D = 1 + 24 = 25
x₁₂ = (1 +- 5)/2 = 3 -2
3 = √9 > √8 не корень
-∛9 < -∛8 = -2 < √8 корень
ответ -2
Похожие вопросы
Предмет: Английский язык,
автор: kisunasaba111
Предмет: Английский язык,
автор: 1Вика111
Предмет: Окружающий мир,
автор: АсемаШиманова1
Предмет: Английский язык,
автор: Marianna9392829
Предмет: Математика,
автор: MashaLove12