Предмет: Математика,
автор: VIPpersona777
Найдите неопределённый интеграл:
Приложения:
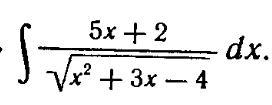
Ответы
Автор ответа:
0
Ответ:
В числителе делаем производную знаменателя
Похожие вопросы
Предмет: Русский язык,
автор: Лев651
Предмет: Русский язык,
автор: Nasovanohkmamb
Предмет: Русский язык,
автор: kristinochka2999
Предмет: Английский язык,
автор: ibragimchadiev
Предмет: Другие предметы,
автор: qwerty123110