Предмет: Математика,
автор: HOLTZMANN1
ПОМОГИТЕ, ПОЖАЛУЙСТА, ВЫЧИСЛИТЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ
Приложения:
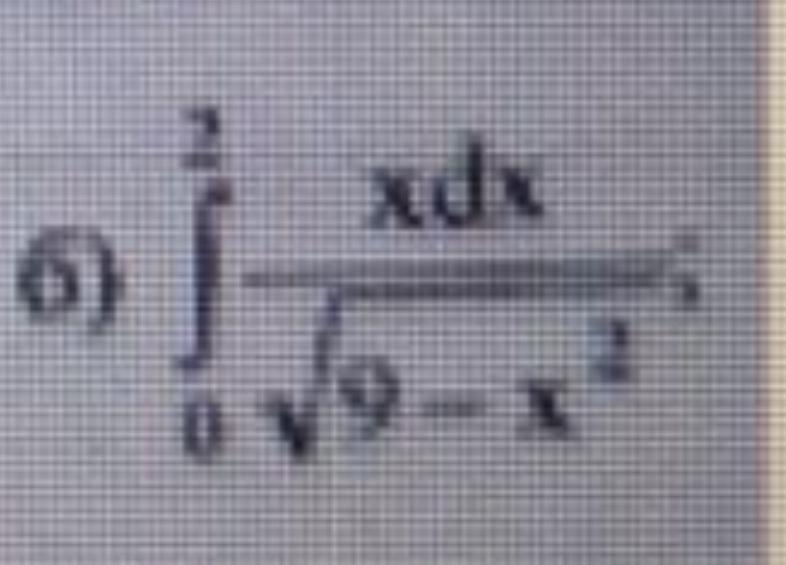

Ответы
Автор ответа:
0
Ответ:
По частям:
Похожие вопросы
Предмет: Английский язык,
автор: kuka2
Предмет: Русский язык,
автор: aizada0498
Предмет: Окружающий мир,
автор: polinazaytseva2
Предмет: Математика,
автор: Zigzag12f
Предмет: Английский язык,
автор: КрутойПарень123