Предмет: Алгебра,
автор: fruztania
1. Упростить выражение 
Варианты ответов:
а) 
б) -1
в) a – 1
г) 
2. Упростить выражение 
Варианты ответов:
а) 
б) 
в) 
г) 
3. Из формулы  выразить переменную b через переменные a и c.
выразить переменную b через переменные a и c.
Варианты ответов:
а) 
б) 
в) 
г) 
4. Вычислить значение выражения  если
если 
Варианты ответов:
а) 0,5
б) 5
в) 0,2
г) 2
Ответы
Автор ответа:
2
1.
2.
3.
4.
fruztania:
Огромное спасибо!)))
Автор ответа:
2
Ответ: 1) в; 2) б; 3) а; 4) в
Решение смотрите на фотографии
Приложения:
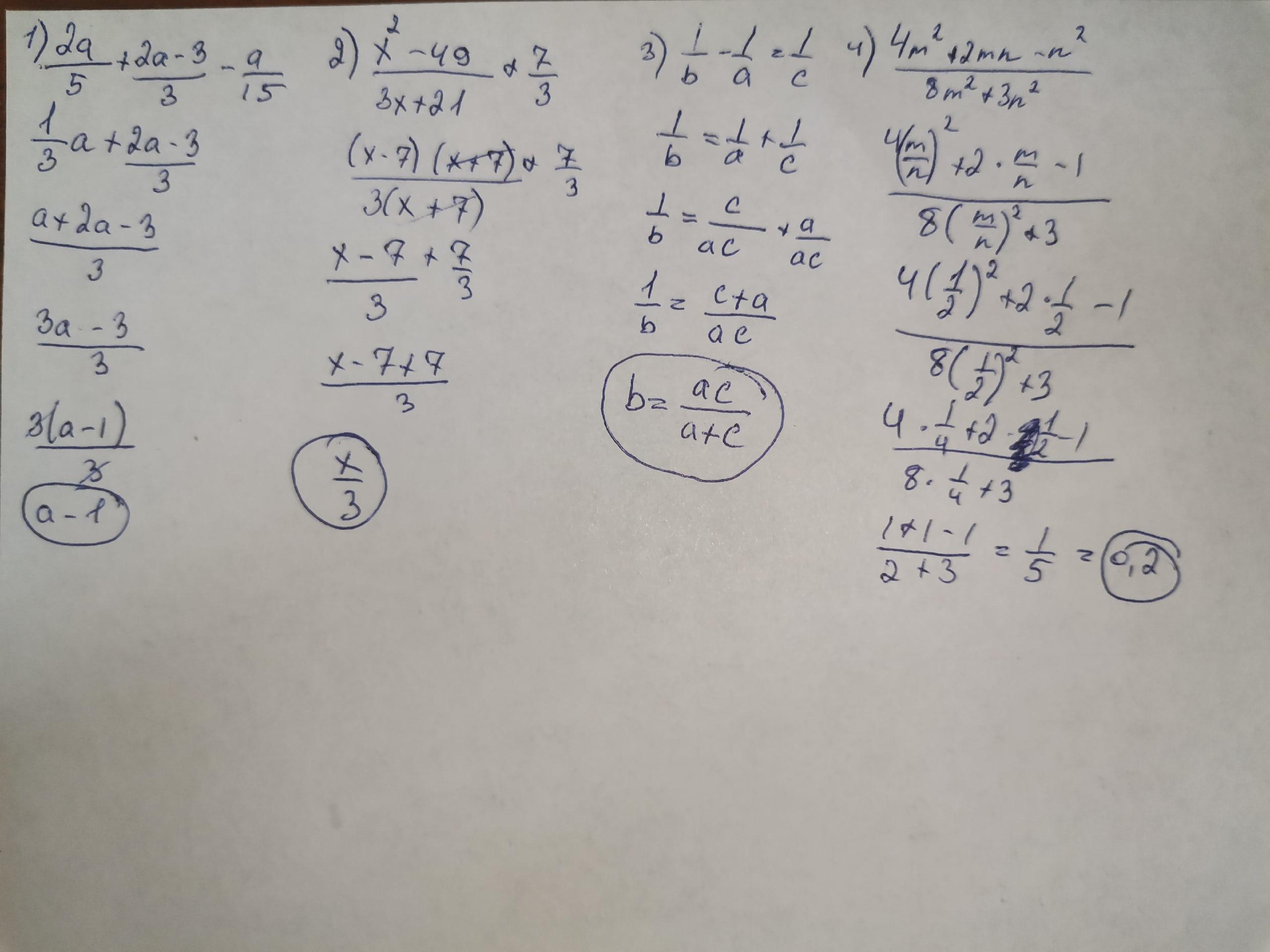
Огромное спасибо!)))
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Камила77
Предмет: Қазақ тiлi,
автор: loa444555
Предмет: Математика,
автор: snoopy24
Предмет: Геометрия,
автор: IMTANDER