Question

2) Найти длину бокового ребра правильной четырехугольной пирамиды, если сторона ее основания и высоты соответственно равны 12 и 3 см
А) √66
Б) 6√2
В) 9
Г) 8√2

3) Найти длину бокового ребра правильной четырехугольной пирамиды, если сторона ее основания и высоты соответственно равны 10 и 4 см
А) √66
Б) 6√2
В) 9
Г) 8√2

Answer 1

смотрим приложение!

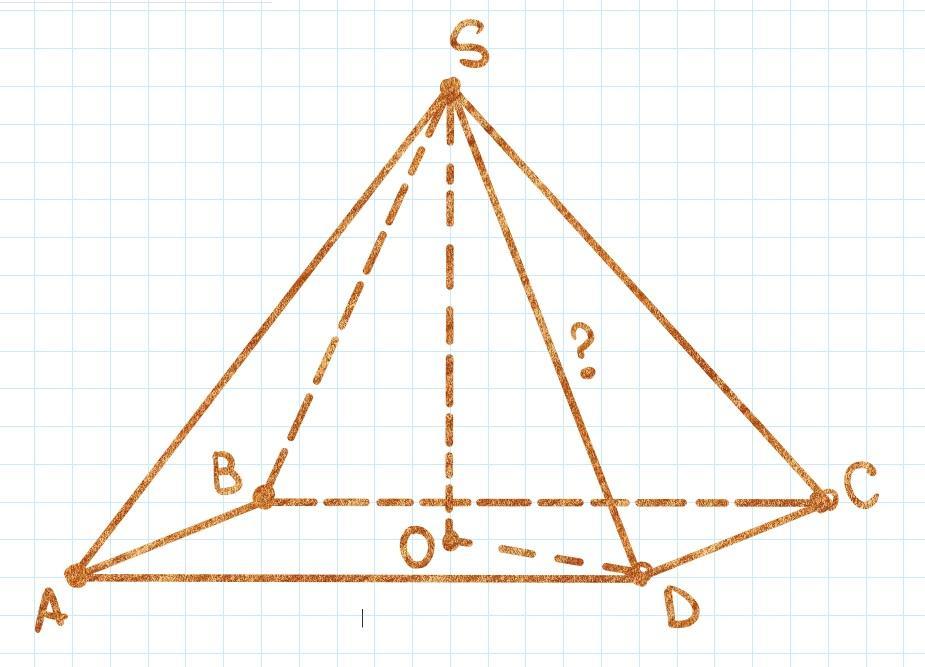
пусть a - сторона основания, h - высота пирамиды

OD - половина диагонали основания, то есть OD = 0,5 · a ·√2

(диагональ квадрата со стороной a равна a√2)

ΔSOD - прямоугольный (∠O = 90°) ⇒ SD² = SO² + OD² (теорема Пифагора)

SD² = h² + 0,5a²

2) h = 3 см, a = 12 см

OD = 6√2

SD² = 9 + 72; SD² = 81; SD = 9 (ответ В)

3) h = 4 см, a = 10 см

OD = 5√2

SD² = 16 + 50 = 66; SD = √66 (ответ А)