Предмет: Алгебра,
автор: Dreamcatcher579
Вычислить дифференциальное уравнение первого порядка:
Приложения:
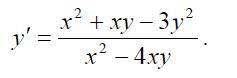
Ответы
Автор ответа:
1
Ответ:
Это однородное ДУ
общее решение
Dreamcatcher579:
большое спасибо))) чтот я сам не сразу вспомнил про этот способ хых
Похожие вопросы
Предмет: Английский язык,
автор: Squirelli
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: Kolyachornogal
Предмет: Математика,
автор: SonyaShishparenko
Предмет: Математика,
автор: kamila10101001