Question

Найдите координаты точек пересечения двух окружностей СРООООООЧНООООО ПОМОГИИИИТЕЕЕЕЕ ПОЖАЛУЙСТА Даю 20 баллов ​

Answer 1

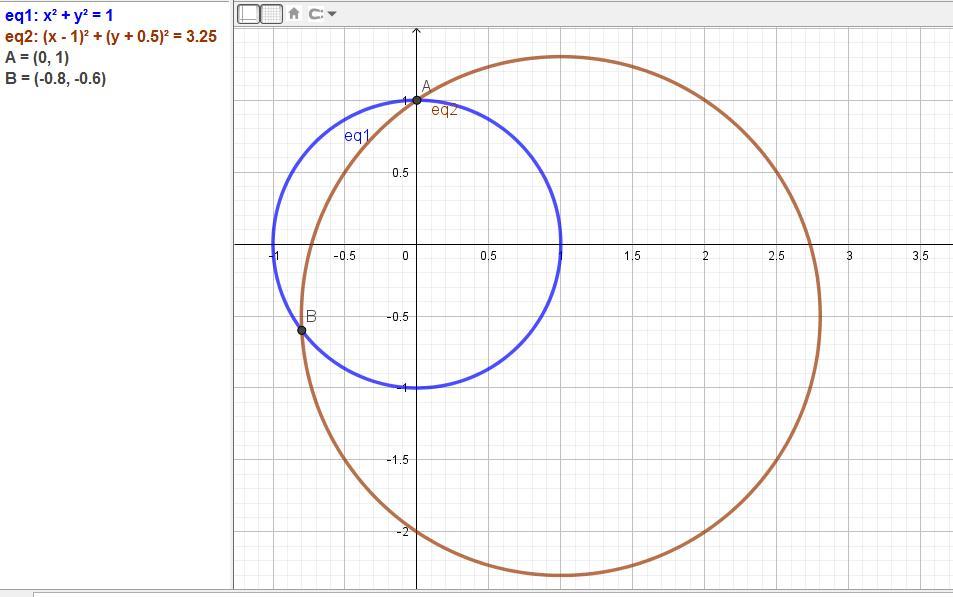
Даны уравнения окружностей:

x² + y² = 1,

x² + y² - 2x + y - 2 = 0.

Используем способ подстановки.

x² = 1 - y² и x = √(1 - y²).

1 - y² + y² + 2√(1 - y²) + y - 2 = 0,

y - 1 = 2√(1 - y²), возведём обе части в квадрат.

y² - 2y + 1 = 4 - 4y²,

5y² - 2y - 3 = 0.

Ищем дискриминант:

D=(-2)^2-4*5*(-3)=4-4*5*(-3)=4-20*(-3)=4-(-20*3)=4-(-60)=4+60=64;

Дискриминант больше 0, уравнение имеет 2 корня:

y_1=(√64-(-2))/(2*5)=(8-(-2))/(2*5)=(8+2)/(2*5)=10/(2*5)=10/10=1;

y_2=(-√64-(-2))/(2*5)=(-8-(-2))/(2*5)=(-8+2)/(2*5)=-6/(2*5)=-6/10=-0.6.

Находим значение x:

x_1 = √(1 - 1) = 0,

x_2 = √(1 - 0,36) = √0,64 = +-0,8.

По второму уравнению подходит значение x_2 = -0,8.

Ответ: A(0; 1), B(-0,8; -0,6).