Предмет: Геометрия,
автор: lerashin5100
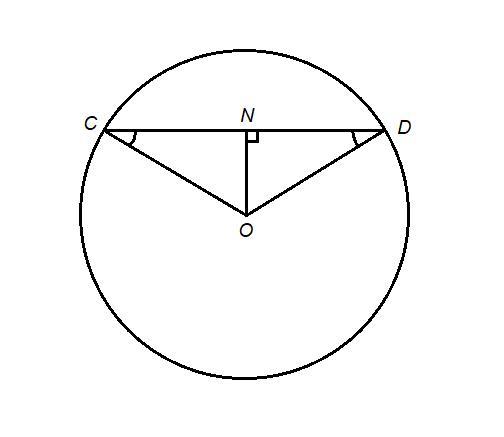
Дана окружность с центром о. длина перпендикуляра on, подведенного к хорде dc данной окружности, равна 12 см. вычислите радиус данной окружности, если сумма углов odn и nco равна 60 градусов.
Ответы
Автор ответа:
2
Ответ:
24 см
Объяснение:
DC - хорда окружности,
ON⊥DC, ON = 12 см
∠ODN + ∠NCO = 60°
Найти радиус окружности.
Проведем OD и ОС - радиусы.
OD = OC, ΔOCD равнобедренный с основанием DC.
- Углы при основании равнобедренного треугольника равны.
∠ODN = ∠NCO = 60° : 2 = 30°
ΔOCN: ∠ONC = 90°, ∠NCO = 30° (ON⊥DC по условию), значит
ON = 0,5 OC по свойству катета, лежащего против угла в 30°.
ОС = 2ON = 2 · 12 = 24 см
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Катя51111
Предмет: Русский язык,
автор: TheAmina17
Предмет: Українська мова,
автор: план8
Предмет: Русский язык,
автор: делания
Предмет: Математика,
автор: лера2300