Предмет: Алгебра,
автор: Davizy
Неравенство (х-а)(4х+1)(х-b) ˃ 0 имеет решение (-∞; -5)ᴗ(-1/4;3). Найдите значения a и b.
Приложения:
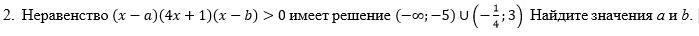
NNNLLL54:
условие точно записано?
да, перепроверял
в условии где-то ошибка
Ответы
Автор ответа:
7
Ответ:
Если задан ответ и неравенство имело
знак ">" , то знаки должны распределяться так:
У неравенства вида ( для определённости
считаем, что a<c<b ) знаки будут распределяться таким образом:
, что никак не соответствует
заданному в условии распределению знаков . В правом промежутке
всегда будет знак (+) , а потом знаки в интервалах будут чередоваться.
Чтобы заданный ответ соответствовал заданному неравенству, надо
было в самом неравенстве записать знак "<" .
Тогда, пусть
Исходя из расстановки знаков получим неравенство уже с конкретны-
ми числами такое:
Сравним неравенства и
и приравняем соответствующие
скобки , получим
Ответ: а) или б)
.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: siv2001
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: elenakulik71
Предмет: Математика,
автор: zheniacaschiri
Предмет: Алгебра,
автор: viktoriya365