Предмет: Геометрия,
автор: snahyu88
прямые АВ АС и АD попарно перпендикулярны найти длину отрезка СD если AD=а, ВС=в, ВD=c
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Дано: AC ⊥ AB, AC ⊥ AD, AD ⊥ AB, AD = а, ВС = b, ВD = c
Найти: CD - ?
Решение:
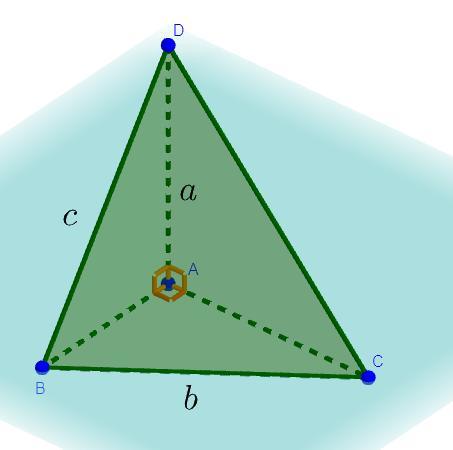
Взаимно перпендикулярные АВ, АС и АD образуют пирамиду ABCD. Тогда по теореме Пифагора для прямоугольных треугольников
ΔABC, ΔADC, ΔABD:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: asemasakura
Предмет: Английский язык,
автор: Nataliachik
Предмет: Английский язык,
автор: marvel2211
Предмет: Алгебра,
автор: eileenclark