Предмет: Алгебра,
автор: Аноним
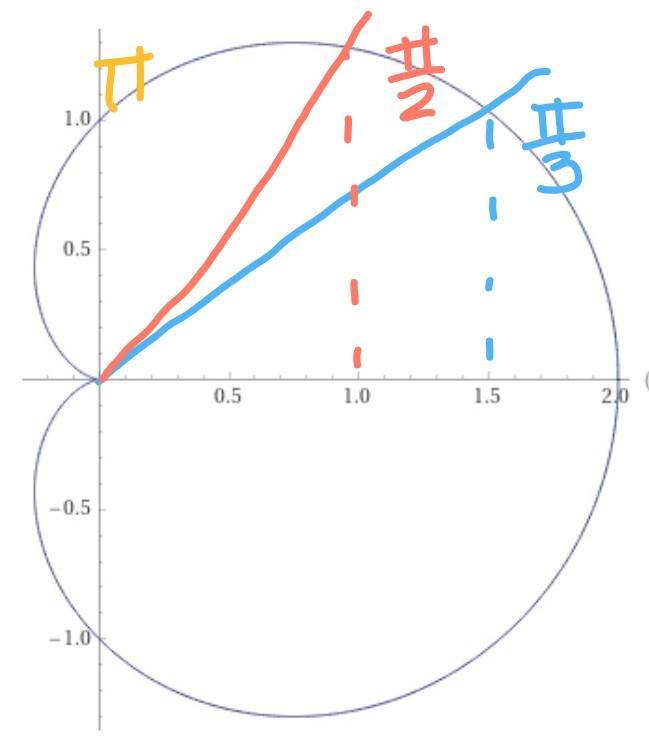
Вычислить площадь фигуры
Приложения:

Ответы
Автор ответа:
0
Ответ:
Область определения:
То есть "фи" - любое
Рисунок
По формуле:
Приложения:
mashhryl:
https://znanija.com/task/44427636 помогите пожалуйста
Похожие вопросы
Предмет: Русский язык,
автор: маша4100
Предмет: Русский язык,
автор: vadim2004mistere
Предмет: Русский язык,
автор: zava2003
Предмет: Окружающий мир,
автор: VikaBolsun2007
Предмет: Математика,
автор: помогите5554653