Предмет: Геометрия,
автор: artemii0302
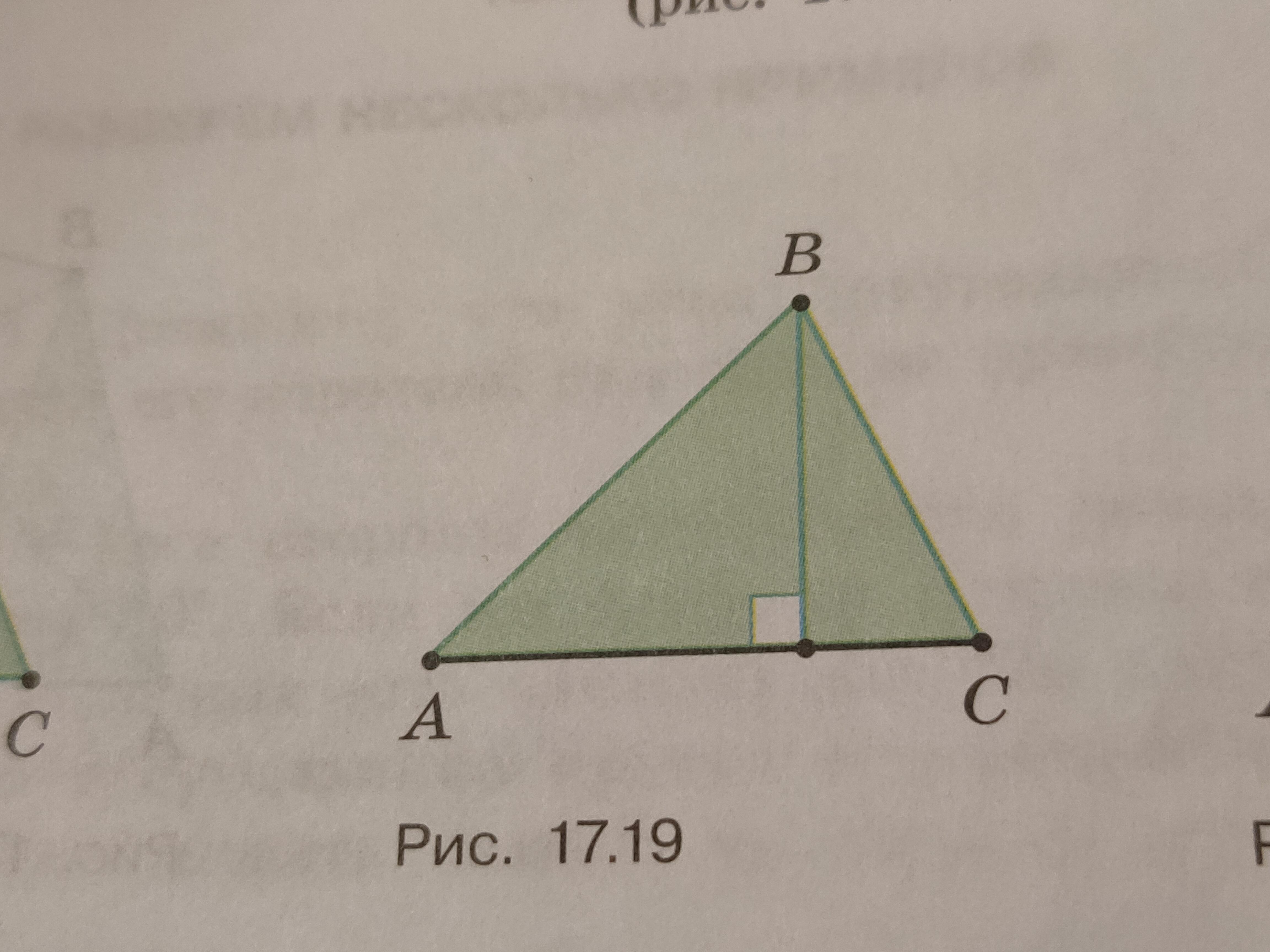
Высота делит сторону неравнобедренного треугольника на два отрезка. Докажите, что меньший из них прилегает к большему углу треугольника (17.19)
Приложения:
Ответы
Автор ответа:
13
Відповідь:
Пояснення:
Один из способов:
В треугольнике напротив большего угла лежит большая сторона.
Провядя высоту ВН, мы получили два прямоугольних треугольника АНВ и СНВ с общим катетом ВН и гипотенузами ВА и ВС- боковими сторонами △АВС → вторые катеты АН и НС, зависят от величини гипотенуз треугольников ВА и ВС, из теореми Пифагора.
Где больше гипотенуза, там и больше второй катет , так как ВН общий катет. А гипотенуза АВ больше ВС, так как лежит против большего угла С и прилежащий угол А есть меншим. И наоборот : меньший катет СН, прилегает к большему углу С △АВС
Похожие вопросы
Предмет: Английский язык,
автор: 9835
Предмет: Французский язык,
автор: dashak2003k
Предмет: Русский язык,
автор: AlinKa20021111
Предмет: Русский язык,
автор: Mrdanik17
Предмет: Биология,
автор: Sinbod