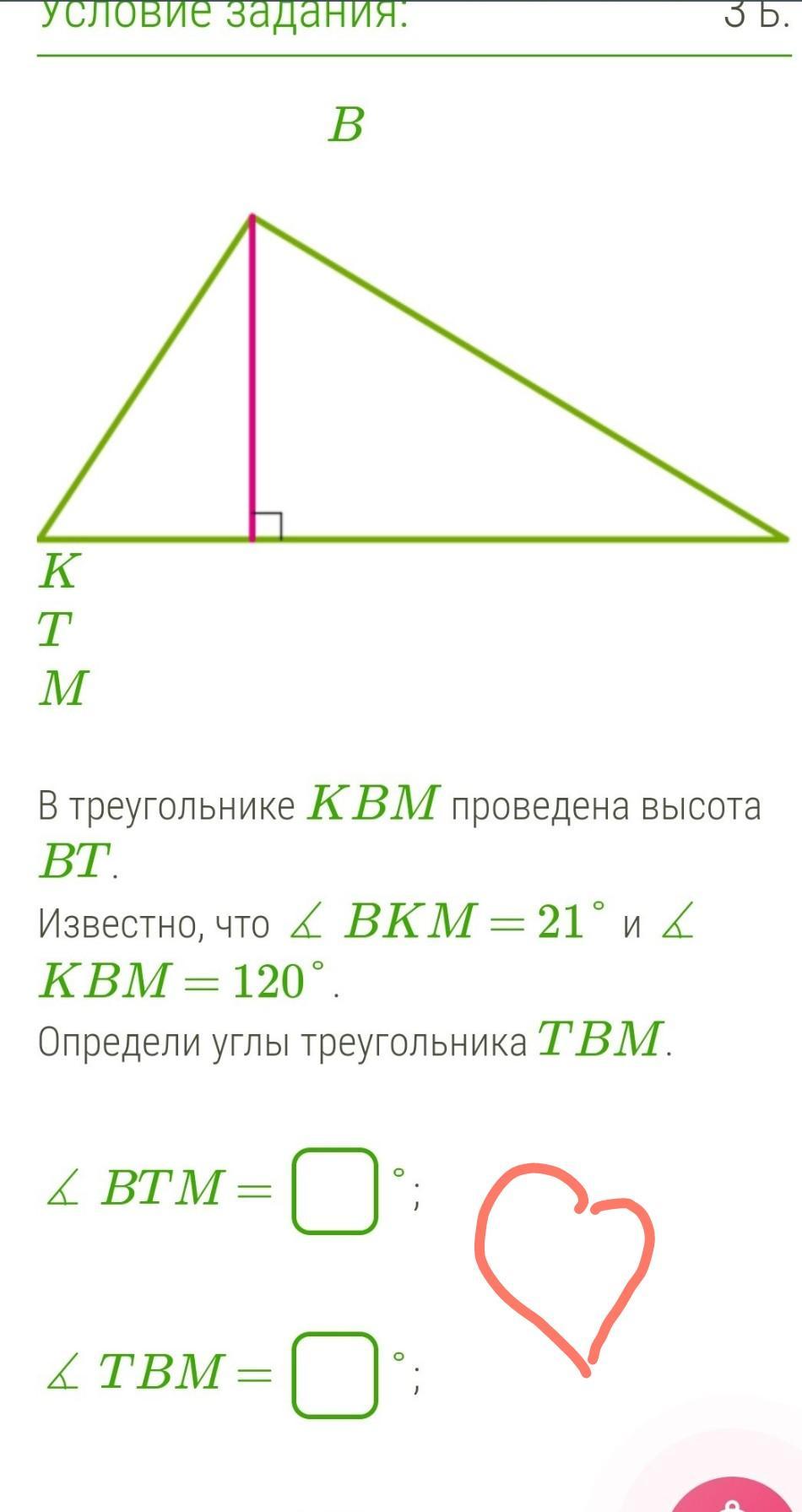
В треугольнике KBM проведена высота BT.
Известно, что ∡ BKM = 21° и ∡ KBM = 120°.
Определи углы треугольника, TBM.
∡ BTM =
°;
∡ TBM =
∡ BMT =
ДАМ 100 БАЛОВ ЗА ПРАВИЛЬНЫЙ ОТВЕТ ПЖ
Ответы
Ответ:
∠ВТМ = 90°,
∠ТВМ = 51°;
∠ВМТ = 39°.
Объяснение:
Первый способ решения
1) Сумма внутренних углов треугольника КВМ равна 180°.
Следовательно:
∠ВМК = 180° - ∠ВКМ - ∠КВМ = 180° - 21° - 120° = 39°.
Так как стороны угла ВМТ треугольника ТВМ совпадают со сторонами угла ВМК треугольника КВМ, то:
∠ВМТ = ∠ВМК = 39°.
2) ∠ВТМ = 90°, т.к. ВТ⊥ТМ (согласно условию).
3) ∠ТВМ = 90° - ∠ВМТ = 90° - 39° = 51°.
Ответ: углы треугольника ТВМ равны:
∠ВТМ = 90°,
∠ТВМ = 51°;
∠ВМТ = 39°.
Второй способ решения
1) Рассмотрим Δ ВКТ:
а) ∠ВКТ = 21°, т.к. стороны угла ∠ВКТ совпадают со сторонами ∠ВКМ = 21°;
b) ∠ВТК = 90°, т.к. ВТ⊥КТ (согласно условию);
с) ∠КВТ = 90° - ∠ВКТ = 90° - 21° = 69°.
2) Рассмотрим Δ ТВМ:
а) ∠ТВМ = ∠КВМ - ∠КВТ = 120° - 69° = 51°;
b) ∠ВТМ = 90°, т.к. ВТ⊥ТМ (согласно условию);
с) ∠ВМТ = 90° - ∠ТВМ = 90° - 51° = 39°.
Ответ: углы треугольника ТВМ равны:
∠ВТМ = 90°,
∠ТВМ = 51°;
∠ВМТ = 39°.