Question

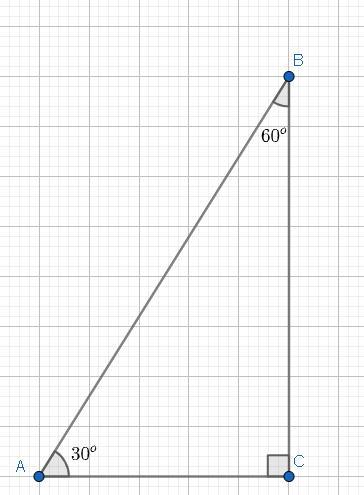
1. Дан прямоугольный треугольник ABC, 2C = 90°
ZB= 60 °, AB+CB=24 см. Найти AB и CB.​

Answer 1

<B = 60° ⇒ <A = 90-60 = 30°.

Нам известны все углы прямоугольного треугольника.

Теорема о 30-градусном угле прямоугольного треугольника такова: Катет, противолежащий углу 30-градусов — равен половине гипотенузы.

Напротив угла A — стоит катет BC, то есть: $<A = 30^o \Rightarrow BC = AB/2.$

Первое условие было таково: $AB + CB = 24cm.$

Мы определили второе условие: $BC = AB/2.$

Из этого следует, что обе стороны имеют одну и те жу переменную.

Можем составить уравнение, с переменными: (BC = x/2); (AB = x):

$\displaystyle\\\\x+x/2 = 24\\\\\frac{x}{1}+\frac{x}{2} = \frac{2x}{2}+\frac{x}{2} = \frac{3x}{2}\\\\3x/2 = 24\\3x = 24*2 \\3x = 48 \Rightarrow\\x = 48/3 = 16cm\\\\x/2 = 16/2 = 8cm \Longrightarrow\\\\AB = 16cm; BC = 8cm.$

Вывод: AB = 16см; BC = 8см.