Предмет: Математика,
автор: 89Oleg89
Сделайте задачу пожалуйста
Приложения:
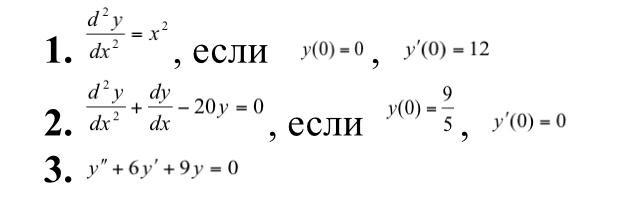
Ответы
Автор ответа:
1
Ответ:
1.
общее решение
частное решение
2.
общее решение
частное решение
3.
общее решение
Похожие вопросы
Предмет: Английский язык,
автор: elenakofman
Предмет: Русский язык,
автор: Вячеслав382847
Предмет: Қазақ тiлi,
автор: andriana200
Предмет: Математика,
автор: Diana101312
Предмет: Математика,
автор: Likpeel2017