Предмет: Математика,
автор: russkihdan2004
Надо вычислить производную, помогите пожалуйста, очень срочно надо
Приложения:
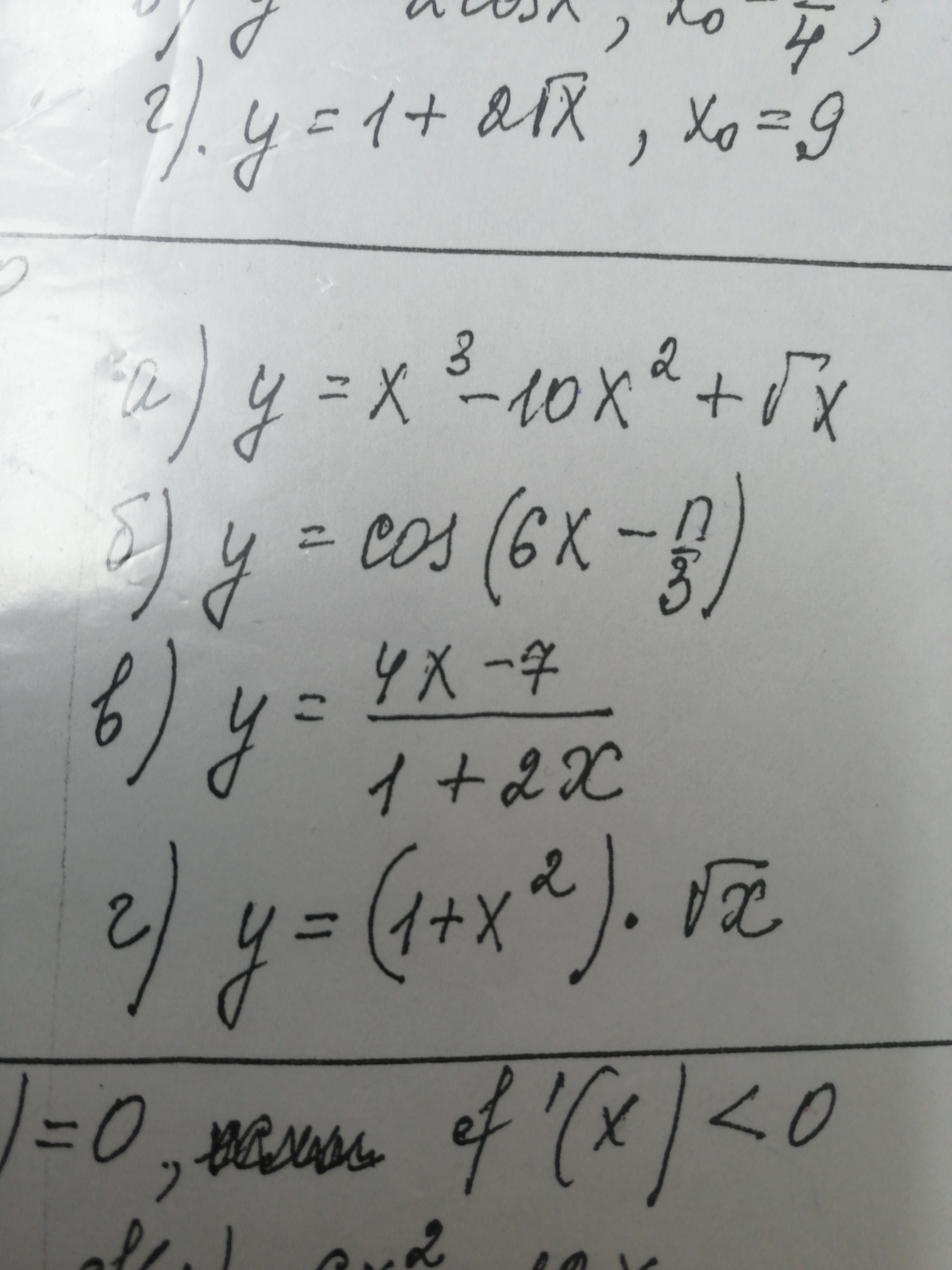
Ответы
Автор ответа:
2
Ответ:
a
б
в
г
Похожие вопросы
Предмет: Английский язык,
автор: karinkaac
Предмет: Русский язык,
автор: ольчик60
Предмет: Русский язык,
автор: fuewe8wnushh
Предмет: Немецкий язык,
автор: nasrya2
Предмет: Литература,
автор: mussa77777