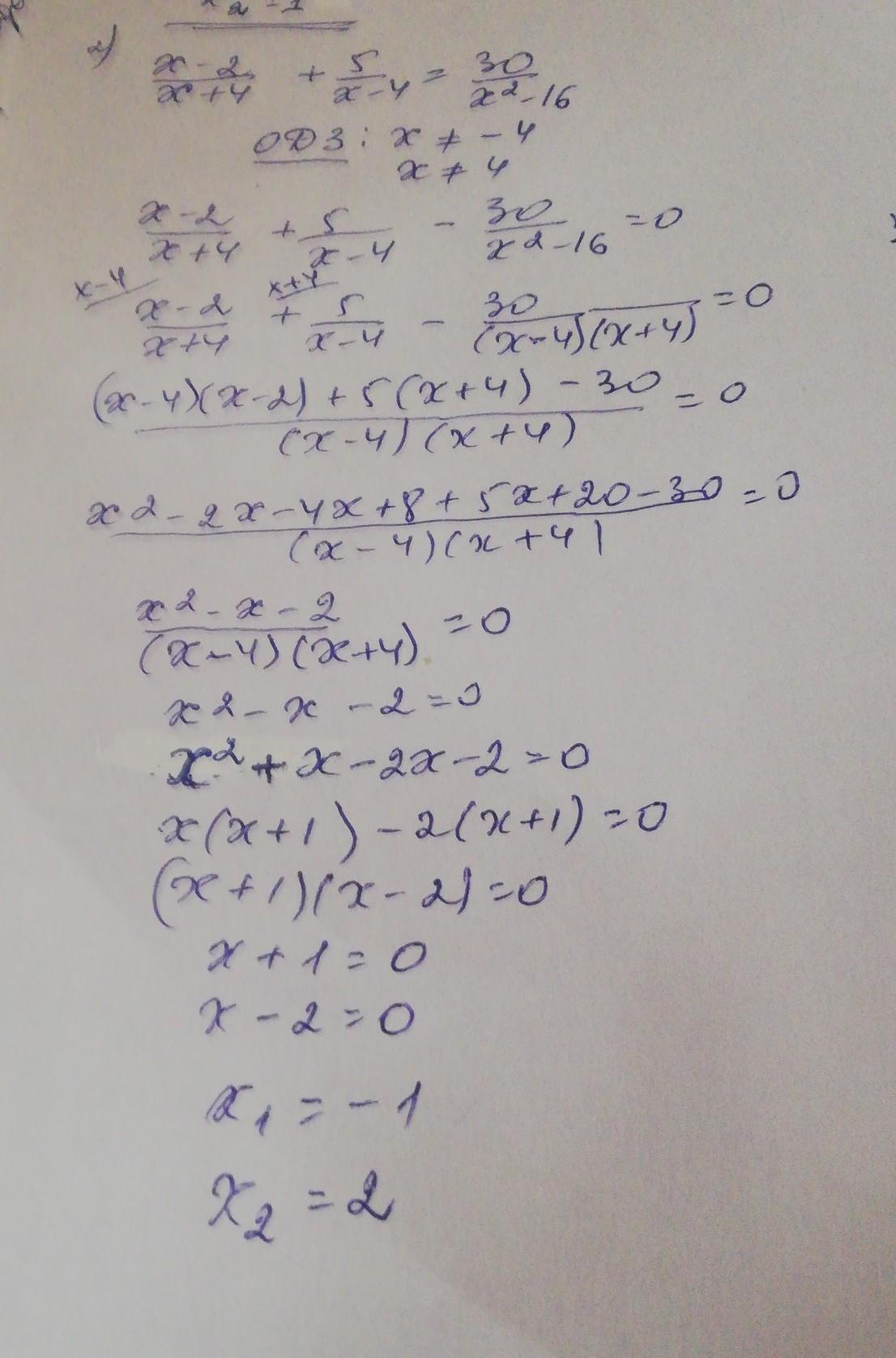Question

1) Корнем уравнения $\frac{x^{2} +5x}{x-6} = \frac{6}{x-6}$ является числа (число)....
Варианты ответов:
а) 2; 3
б) -6; 1
в) 6
г) -1; 6

2) Определить квадратное уравнение, к которому сводится дробно-рациональное уравнение $\frac{x-2}{x+4} + \frac{5}{x-4} =\frac{30}{x^{2}-16}$
Варианты ответов:
а) $x^{2} -11x-30=0$
б) $x^{2} -x-2=0$
в) $x^{2} +x-2=0$
г) $x^{2} +x-12=0$

3) Образования квадратное уравнение, выполняя равносильно преобразования на всей области определения уравнения.
$\frac{3x+11}{x+2} -\frac{2x-9}{x-4} =7$
Варианты ответов:
а) $x^{2}$ - 3x - 5 = 0
б) 2$x^{2}$ + 10x - 6 = 0
в) 5$x^{2}$ + 8x - 6 = 0
г) 2$x^{2}$ - 10x + 6 = 0

Answer 1

Ответ:

1.  Б -6; 1

2. Б ${x}^{2} - x - 2 = 0$

3. А   ${x}^{2} - 3x - 5 = 0$

Детальнее:

1. Область допустимых значений: $x\neq 6$

Когда знаменатели одинаковые, можно

сравнить числительные: $x^{2} +5x=6$

Переносим число с противоположным значением в левую часть, чтобы получилось квадратное уравнение и решаем:

$x^{2} +5x-6=0\\D=b^{2}-4ac=5^{2} -4*1*(-6)=25+24=49\\\sqrt{D}=\sqrt{49}=7$

x₁ $=\frac{-b-\sqrt{D} }{2a}=\frac{-5-7}{2}=\frac{-12}{2} =-6$

x₂ $=\frac{-b+\sqrt{D} }{2a} = \frac{-5+7}{2} =\frac{2}{2}=1$

Условие соблюдено: $x\neq 6$

Ответ: x₁ = -6; x₂ = 1.

2. Область допустимых значений: $x\neq -4, x\neq 4$

Переносим число с противоположным значением в левую часть, чтобы получилось квадратное уравнение и решаем:

$\frac{x-2}{x+4}+\frac{5}{x-4}-\frac{30}{x^{2} -16} =0\\\frac{x-2}{x+4}+\frac{5}{x-4}-\frac{30}{(x-4)(x+4)} =0\\\frac{(x-4)(x-2)+5(x-4)-30}{(x-4)(x+4)} =0\\\frac{x^{2} -2x-4x+8+5x+20-30}{(x-4)(x+4)} =0\\\frac{x^{2} -x-2}{(x-4)(x+4)} =0$

Когда частное двух выражений равна нулю, то числитель должен быть равным нулю:

$x^{2} -x-2=0$

3. Область допустимых значений: $x\neq -2, x\neq 4$

Переносим число с противоположным значением в левую часть, чтобы получилось квадратное уравнение и решаем:

$\frac{3x+11}{x+2}-\frac{2x-9}{x-4}-7=0\\\frac{(x-4)(3x+11)-(x+2)(2x-9)-(7(x+2)(x-4)}{(x+2)(x-4)} =0\\\frac{3x^{2}+11x-12x-44-(2x^{2}-9x+4x-18)+(-7x-14)(x-4) }{(x+2)(x-4)} =0\\\frac{3x^{2}+11x-12x-44-2x^{2} +5x+18-7x^{2} +28x-14x+56 }{(x+2)(x-4)} =0\\\frac{-6x^{2} +18x+30}{(x+2)(x-4)} =0$

Когда частное двух выражений равна нулю, то числитель должен быть равным нулю:

$-6x^{2} +18x+30=0$

Делим обе части уравнения на -6. Получаем:

$x^{2} -3x-5=0$

Answer 2

Ответ:1)б 2)б 3)а

Смотри решение на фото