Предмет: Математика,
автор: kuanishbayevyernazar
Всем привет. Пожалуйста помоги!
Найдите специальные
производные вышеупомянутой комплексной функции.
Приложения:
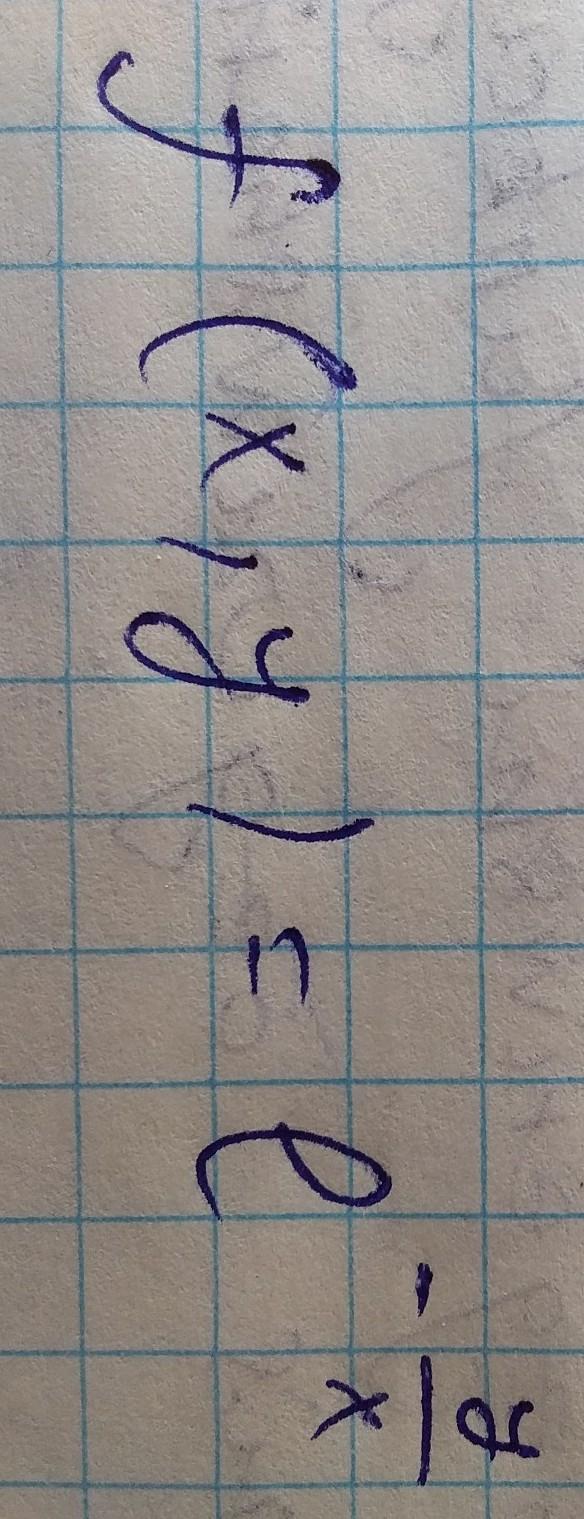
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
функция задана неявно
ищем производную по формуле
kuanishbayevyernazar:
Спасибо ☺️
пожалуйста -))
Похожие вопросы
Предмет: Русский язык,
автор: салта9
Предмет: Английский язык,
автор: kovalev2005
Предмет: Русский язык,
автор: димадава
Предмет: Английский язык,
автор: Аришка2311
Предмет: Алгебра,
автор: alinnedenisenko