Question

Внутри прямого угла BAC проведён луч AK, который делит угол BAC в отношении 2:1. Найдите угол между биссектрисами углов BAK и CAK

Answer 1

Ответ:

45°

Объяснение:

∠ВАК=х°,  ∠КАС=2х°

х+2х=90;  3х=90;  х=30

∠ВАК=30°,  ∠КАС=60°

Пусть АМ - биссектриса ∠ВАК, АР - биссектриса ∠САК, тогда

∠МАР=1/2 ∠ВАК + 1/2 ∠КАС = 15 + 30 = 45°

Answer 2

Ответ:

Объяснение:

1) ∠ВАК : ∠КАС = 2 : 1

∠А = ∠ВАК +∠КАС = 2 + 1 = 3(части) = 90°

∠КАС = 90°/3 = 30°

∠ВАК = 30° * 2 = 60°

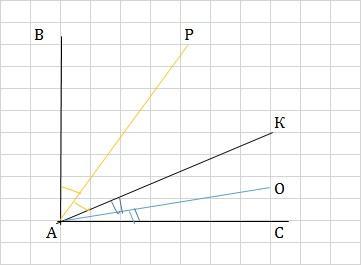
2)  АР - биссектриса ∠ ВАК, значит,

∠ВАР = ∠РАК = 60°/2 = 30°

АО - биссектриса угла ∠КОС, следовательно,

∠КАО = ∠ОАС = 30° / 2 = 15°

3) ∠РАО = ∠РАК + ∠КАО = 30° + 15° = 45°