Люди добрые! Нужна помощь по РЯДАМ! 45 баллов.
В первых двух заданиях сходимость найти. А в 3 разложение по степеням. Не знаю как делать, потому что проболел...
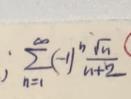
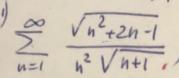
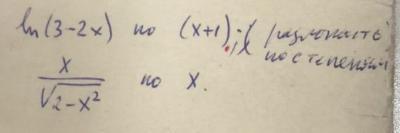
Ответы
Ответ:
Пошаговое объяснение:
1)
для знакочередующегося ряда применим признак Лейбница:
если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится
а) (-1)¹*(1/3); √2/4; (-1)³(√3/5; ..... ряд знакочередующийся
б)
применим сравнительный признак: α=1/2
α < 1, ряд расходится
ответ
исходный ряд расходится
2)
рассмотрим предел
применим сравнительный признак α=2
α > 1, - ряд сходится
3) формула
функция ln(32x) по степеням (х+1)
поскольку у нас логарифм, то можно было бы использовать известное разложение логарифма ln(1+x) и "подогнать" наш логарифм под этот, но мне такой путь показался сложнее, чем обычный
итак, разложение
найдем значения функции и ее производных при х=(-1)
f(x)=ln(3-2x), f(-1)=ln(5)
таким образом мы получаем ряд
или
второй случай похуже будет
и тем не менее
функция по степеням х
находим значение функции и производных в точке 0
тогда получаем ряд
теперь самое противное - формула членов ряда
вот такая вот фигнень....
(n-1) mod 2 - это значит (n-1) - четное
otherwise - значит в любом другом случае