Предмет: Геометрия,
автор: panchenkocofia2016
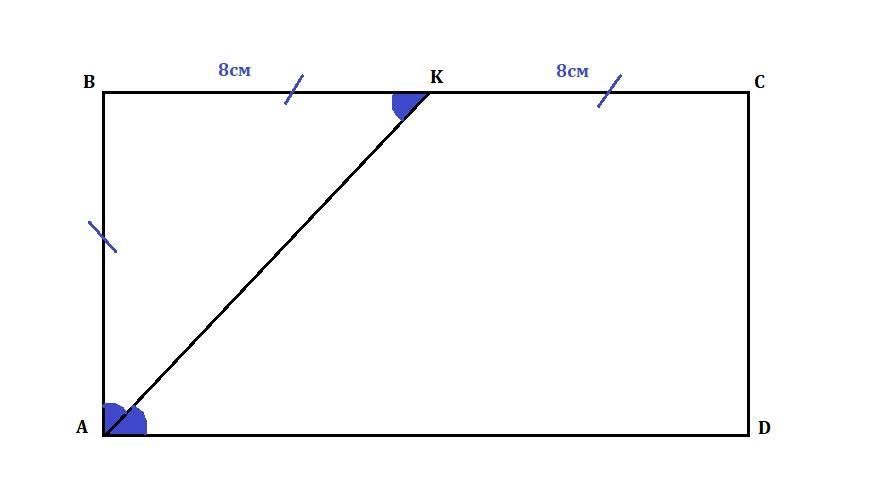
Бісектриса кута А прямокутника ABCD перетинає сторону ВС в точці К.
Обчисліть площу чотирикутника AKCD , якщо ВК=KC=8см. *
Надати повний розв'язок
Ответы
Автор ответа:
13
Ответ:
S(AKCD) = 96 см²
Объяснение:
Так як АК - бісектриса, то ∠ВАК=∠DAK.
ABCD - прямокутник. ⇒ Його протилежні сторони рівні та паралельні.
- Якщо в прямокутнику проведена бісектриса, яка перетинає одну зі сторін, то вона відтинає від прямокутника рівнобедрений трикутник.
Так як ВС║АD, то ∠ВКА=∠DAK - як внутрішні різносторонні кути при січній АК. ⇒ ∠ВКА = ∠ВАК.
⇒ΔАВК - рівнобедрений. АВ=ВК=8 см
Чотирикутник AKCD є прямокутною трапецією. Основа КС=8см, основа АD=ВС=ВК+КС=8+8=16см, висота СD=АВ=8см.
Площу трапеції знаходимо за формулою:
см²
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: 5555597
Предмет: Українська мова,
автор: martyha380
Предмет: Русский язык,
автор: dimalitvyak
Предмет: Английский язык,
автор: Данил12312
Предмет: Математика,
автор: Infinity167