Предмет: Математика,
автор: Nosferatu7
Здравствуйте. Помогите пожалуйста найти определенный интеграл!
Приложения:
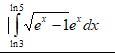
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: elitka200
Предмет: Русский язык,
автор: cabbarli555
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: bezgana
Предмет: Математика,
автор: уличка2008