Question

Пожайлуста помогите !!! Очень срочно даю 38 баллов .​

Answer 1

Ответ:

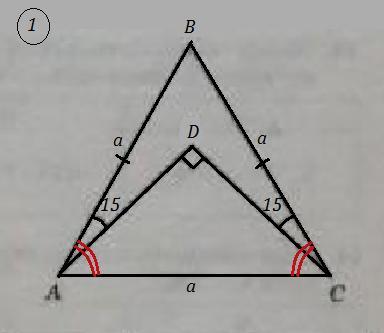
1)  ABCD - четырёхугольник ,  ∠ВАD=∠BCD=15° ,  AB=BC=a .

 Соединим точки А и С, получим ΔАВС - равнобедренный , так как АВ=ВС=а . Поэтому угля при основании ΔАВС равны:  ∠ВАС=∠ВСА .

 В ΔADC  :  ∠ADC=90°  , тогда  ∠DAC+∠DCA=180°-∠ADC=180°-90°=90° .

 Значит, ∠ВАС+∠ВСА=∠BAD+∠BCD+(∠DAC+∠DCA)=15°+15°+90°=120° .

Тогда  в равнобедренном ΔАВС угол при вершине  ∠В=180°-120°=60°, следовательно и  углы при основании треугольника равны по 60° . Поэтому ΔАВС - равносторонний и все его стороны равны  "а" , AC=a .

Тогда ΔADC - равнобедренный, так как углы при его основании АС равны по 60°-15°=45°  и  AD=DC ,  следовательно

АC=AB·√2  ⇒  a=AB·√2   ,   AB=a:√2

Периметр АВСD равен Р=а+a+(a:√2)+(a:√2)=2a+2·(a:√2)=2a+a·√2 .  

Рис. 1 .

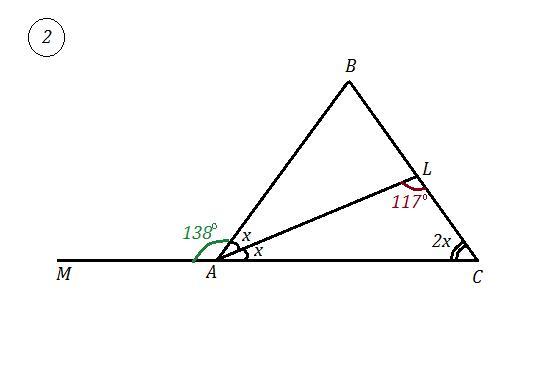
2)  ΔАВС - равнобедренный , АВ=ВС , АL - биссектриса  ⇒  

  ∠BAL=∠CAL  ,  ∠ALB=117° .

 ΔАВС - равнобедренный  ⇒    ∠A=∠C=2x  ,  тогда  ∠BAL=∠CAL=x ,

Рассмотрим ΔALC:  ∠CАL+∠С+∠ALC=180°  ,    x+2x+117°=180°  ,

  3x=63°  ,   x=21°  , ∠С=2х=42°  ,  ∠В=180°-42°-42°=96° .

∠А=∠С=42° как углы при основании равнобедренного треугольника .

Внешний угол при вершине А - это ∠ВАМ .

Он равен 180°-∠А=180°-42°=138° .  

Рис. 2 .