Предмет: Математика,
автор: Jons31
Определить сходимость ряда,
используя признак Даламбера. Желательно с подробныи решением
Приложения:
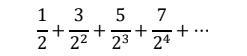
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Даламбер
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования)
у нас ряд
q< 1 ряд сходится
Похожие вопросы
Предмет: Українська література,
автор: vitalybabinin
Предмет: Русский язык,
автор: bubu12
Предмет: Қазақ тiлi,
автор: Astalavista14
Предмет: Алгебра,
автор: Юшка16
Предмет: Математика,
автор: marinaandronov