Question

Помогите ,пожалуйста!
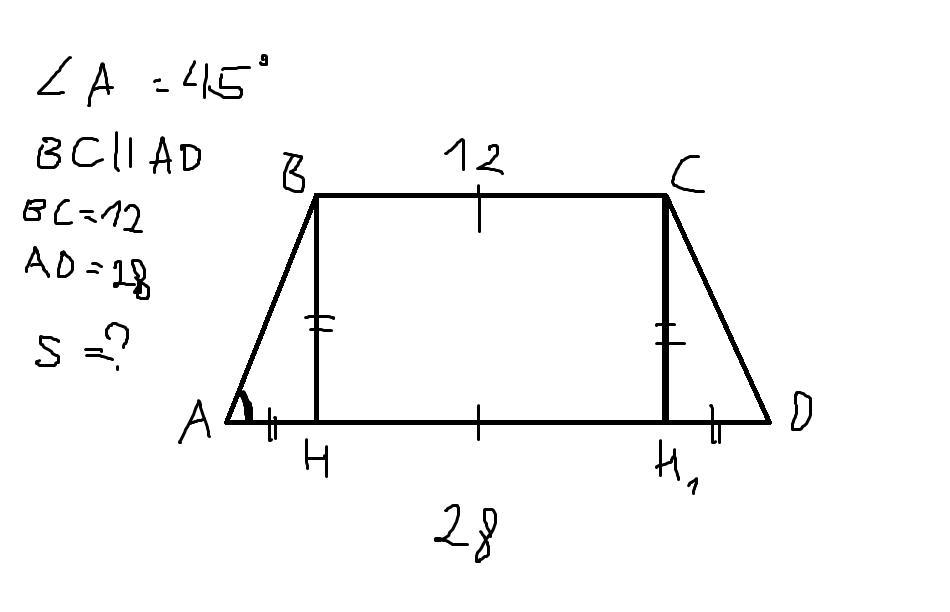
знайдіть площу рівнобічної трапеції якщо її основи дорівнюють 12 см і 28 см а кут при основі 45 .

Answer 1

Ну т.к меньшая основа равна 12, а это равнобокая трапеция, то большую основу можно записать так.

28=12+2x

16=2x

x=8

x - это один из катетов образованных при проведении высот в равнобедренной трапеции.

Т.к в этом треугольнике один угол - 45 градусов

а второй - 90, то третий равен 180-(90+45)=45 градусов.

А т.к два угла равны, то это равнобедренный треугольник.

Значит катеты равны.

А значит высота данной трапеции равна 8 см.

Площадь трапеции - это произведение полсуммы основ на высоту.

Значит

$S=\frac{12+28}{2} *8=160$ см^2

Ответ: 160 см^2

Answer 2

Ответ:

S@=160 cm^2

Объяснение:

Трапеция равнобокая, с углом при основании =45° => h= полуразности оснований= (0,5(а-в).

Sтрап= 0,5(а+в)*h=0,5(a+b)*0,5(a-b)

Sтрап= 1/4(а+b)(a-b)

Sтрап=1/4*(28+12)(28-12)=1/4*40*16

Sтрап=160 см^2