Предмет: Геометрия,
автор: vladsym
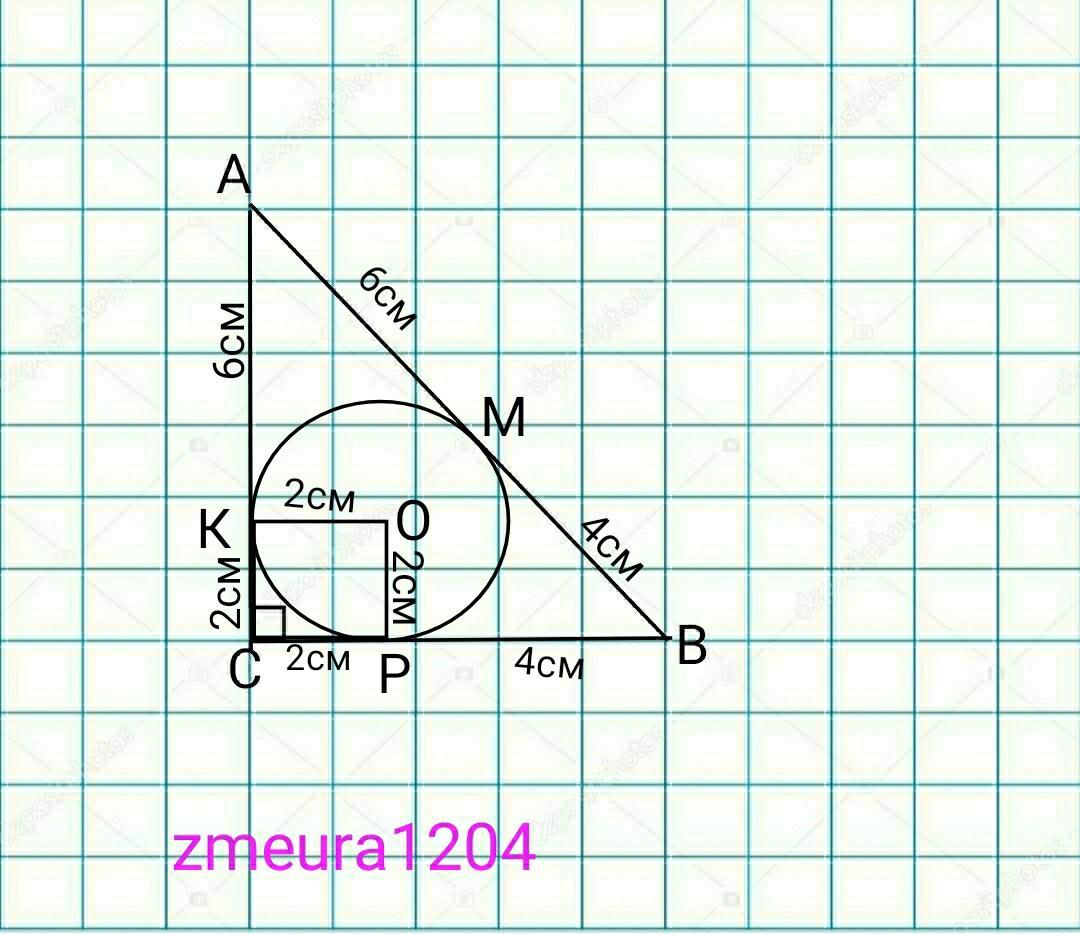
У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки 4 см і 6 см. Знайдіть периметр трикутника, якщо радіус кола дорівнює 2 см.
(В прямоугольном треугольнике точка соприкосновения вписанной окружности делит гипотенузу на отрезки 4 см и 6 см. Найдите периметр треугольника, если радиус окружности равен 2 см.)
Помогите пожалуйста, даю 30 балов
Аноним:
Р=2*4+2*6+2*2=
А конкретнее можно? Ну, расписать подробнее, как геометрическую задачу. Пожалуйста.
Свойство касательных: Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Благодарю!
Ответы
Автор ответа:
7
Ответ:
24см
Объяснение:
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
АМ=АК
МВ=ВР
КС=СР=r
Р=АМ+АК+МВ+ВР+КС+СР=
=2*АМ+2*МВ+2*r=2*4+2*6+2*2=8+12+4=
=24см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: bill100500
Предмет: Английский язык,
автор: cnfccc
Предмет: Русский язык,
автор: ника424
Предмет: Окружающий мир,
автор: rikkir111133