Решить рациональные неравенства
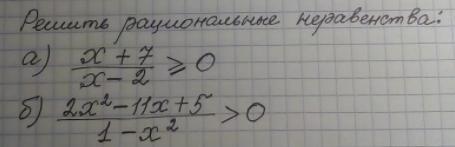
Ответы
Ответ:
В решении.
Объяснение:
а) (х + 7)/(х - 2) >= 0
Решить методом интервалов:
1) Приравнять к нулю и решить уравнение:
(х + 7)/(х - 2) = 0
Умножить обе части уравнения на (х - 2):
х + 7 = 0
х₁ = -7 (кружок закрашенный, нестрогое неравенство);
Знаменатель приравнять к нулю:
х - 2 = 0
х₂ = 2 (кружок будет "выколотым", не закрашенным);
2) На числовой прямой отметить значения -7 и 2;
Определить знак самого правого интервала:
подставить в уравнение х = 3 (любое больше 2):
(3 + 7)/(3 - 2) = 10/1 = 10 >=0, знак плюс.
___________________________________
+ -7 - 2 +
Так как неравенство >= 0, интервалы со знаком + будут решениями данного неравенства:
х∈(-∞; -7] ∪ (2; +∞).
б) (2х² - 11х + 5)/(1 - х²) > 0
Решить методом интервалов:
1) Приравнять к нулю и решить уравнение:
(2х² - 11х + 5)/(1 - х²) = 0
Умножить обе части уравнения на (1 - х²):
2х² - 11х + 5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =121 - 40 = 81 √D=9
х₁=(-b-√D)/2a
х₁=(11-9)/4
х₁=2/4
х₁=0,5;
х₂=(-b+√D)/2a
х₂=(11+9)/4
х₂=20/4
х₂=5;
Знаменатель приравнять к нулю:
1 - х² = 0
(1 - х)(1 + х) = 0
1 - х = 0
-х = -1
х₃ = 1;
1 + х = 0
х₄ = -1.
Отметить все корни на числовой прямой:
_____________________________________________
- -1 + 0,5 - 1 + 5 -
Определить знак самого правого интервала:
подставить в уравнение х = 6 (любое больше 5):
(2*6² - 11*6 + 5)/(1 - 6²) = 1/-35 < 0, значит, минус.
Так как неравенство > 0, решениями будут интервалы со знаком +:
х∈(-1; 0,5) ∪ (1; 5).