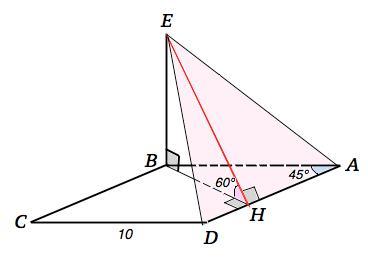
В ромбе АВСD АВ=10 см,<ВАD=45ᵒ, ВЕ перпендикуляр к плоскости АВС. Двугранный угол ЕАDВ равен 60ᵒ. Найдите расстояние от точки Е до плоскости АВС.
Ответы
Ответ: 5√6 см
Объяснение: Решение очень короткое. Вспомним:
1) Двугранный угол - это часть пространства, заключенная между двумя полуплоскостями, имеющими одну общую границу (ребро). Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.
2) Расстоянием от точки до плоскости называется длина перпендикуляра, проведённого из этой точки к плоскости.
3) Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости, и наоборот, если прямая перпендикулярна плоскости, она перпендикулярна любой лежащей в ней прямой.
———————
На рисунке, данном в приложении, ВЕ перпендикулярен к плоскости и потому перпендикулярен высоте ВН к стороне АD. По т. о 3-х перпендикулярах наклонная ЕН перпендикулярна АD, ⇒
∠ ЕНВ =60° ( величина двугранного угла по условию).
∆ НВЕ - прямоугольный, ВН=АВ•sin45°=10•(√2)/2=5√2 ⇒
ВЕ=ВН•tg60°=(5√2)•√3=5√6 см