Предмет: Математика,
автор: Ник531236
Срочно , помогите пожалуйста решить примеры
Приложения:
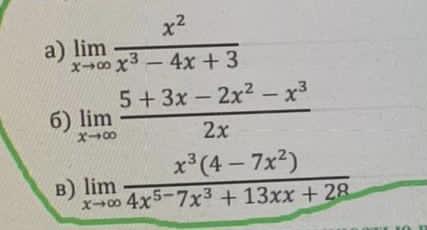
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
a) поделим всё на старшую степень знаменателя
б) делаем все то же самое - делим всё на х
расписывать не буду, тут все понятно
в) сначала упростим дробь а потом опять же поделим всё на высшую степень знаменателя
Похожие вопросы
Предмет: Русский язык,
автор: ЭленМА
Предмет: Английский язык,
автор: Kotonik12
Предмет: Қазақ тiлi,
автор: 6558мед
Предмет: Литература,
автор: Аноним
Предмет: Биология,
автор: Анна123457896