Предмет: Алгебра,
автор: lenyashastin
Ответы
Автор ответа:
1
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
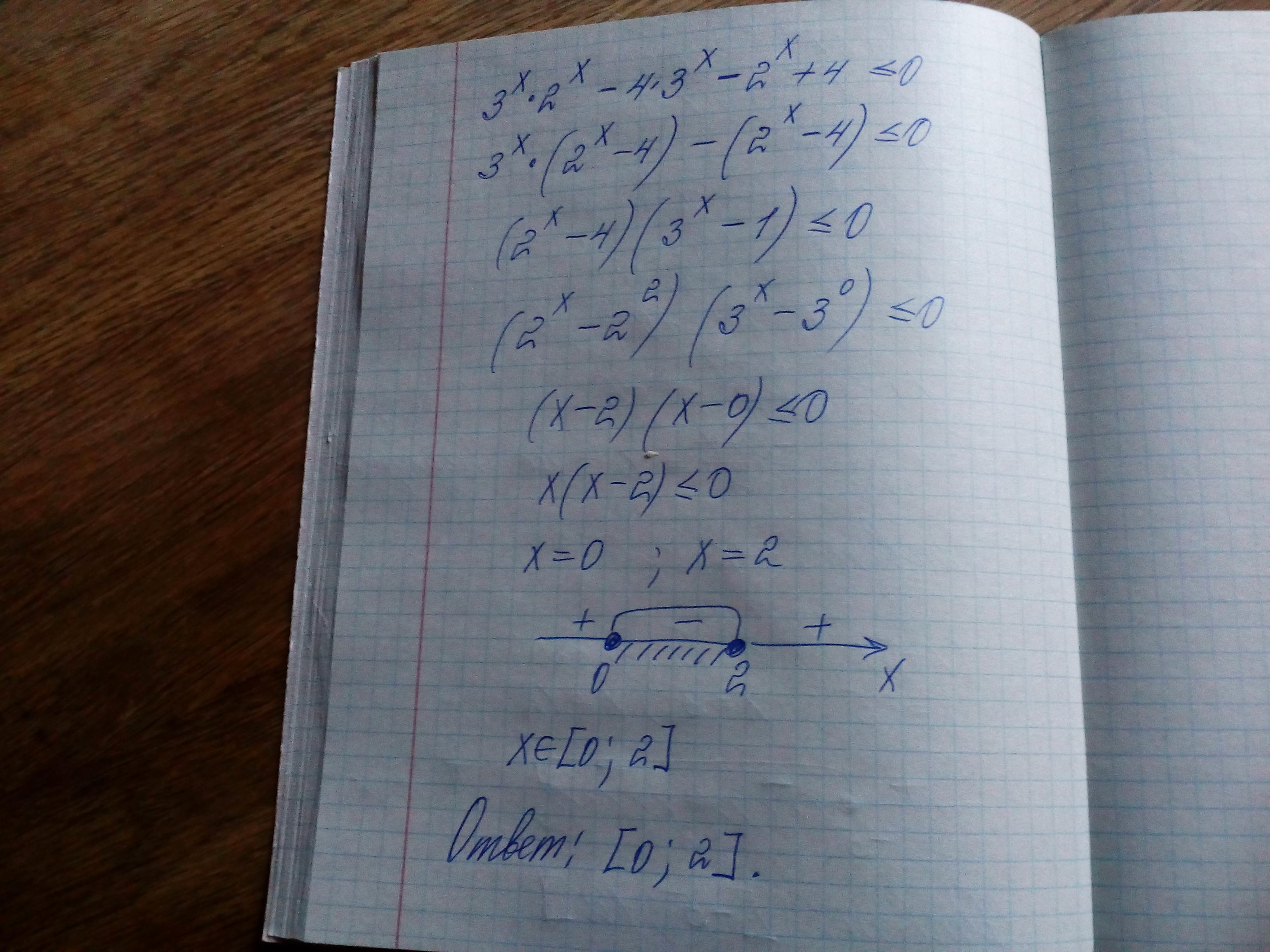
Автор ответа:
3
Ответ:
________________________________
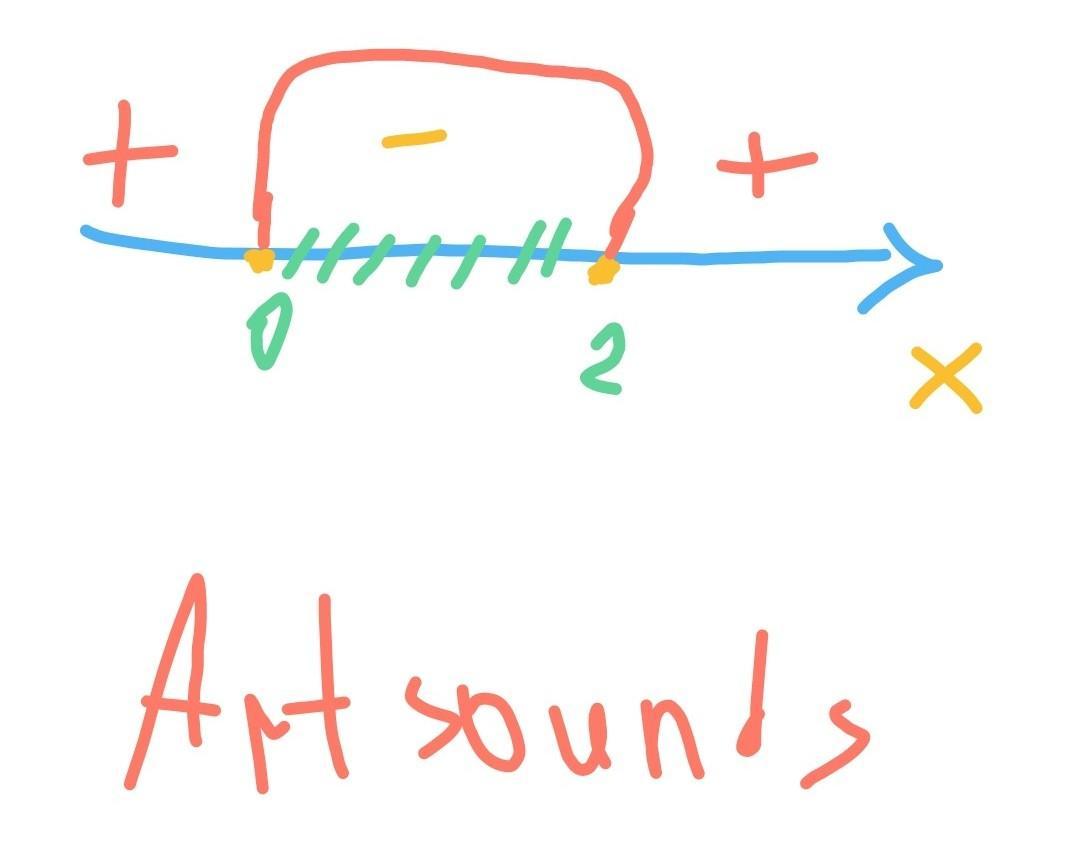
x принадлежит [ 0; 2 ]
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: groznay86
Предмет: Русский язык,
автор: misterklyachin
Предмет: Английский язык,
автор: isakovamarij
Предмет: Право,
автор: doncov2001
Предмет: Русский язык,
автор: Persick19227