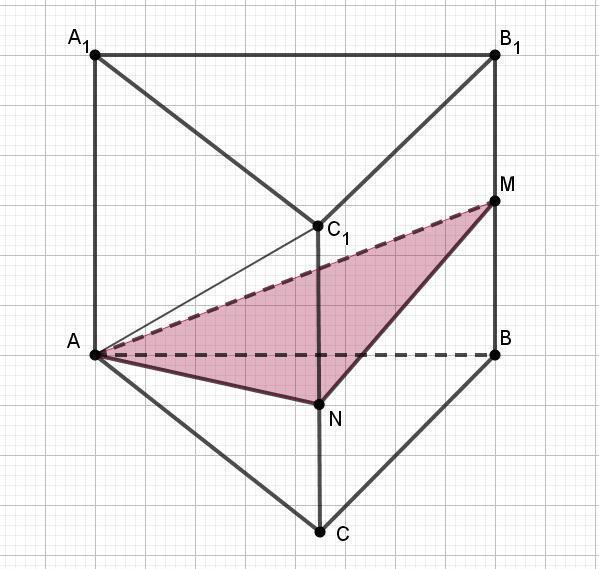
Дана прямая треугольная призма ABCA1B1C1, у которой AC = 6, AA1 = 8. Через вершину A, проведена плоскость, пересекающая ребра BB1 и CC1 соответственно в точках M и N. Найдите в каком отношении делит эта плоскость объем призмы, если известно, что BM = MB1, а AN - биссектриса угла CAC1
С рисунком, пожалуйста)
Ответы
Ответ:
1) Сечение строится по заданным точкам.
Точку N находим в соответствии со свойством биссектрисы (см. пункт 2). Ребро СС1 точкой N делится в отношении 3:5.
2) По заданию AN является биссектрисой угла CAC1.
Диагональ АС1 боковой грани по Пифагору равна √(6² + 8²) = 10.
Примем СN = х.
По свойству биссектрисы х/6 = (8 - х)/10. Сократим знаменатели на 2.
24 - 3х = 5х,
8х = 24,
х = 24/8 = 3.
По заданию ВМ = 8/2 = 4.
Сечение AMN от призмы отсекает пирамиду с основанием BCNM, которое является трапецией (CN ║BM).
S(BCNM) =((3+4)/2)*6 = 21 кв.ед.
Высота H этой пирамиды равна высоте основания АВС.
H = 6*cos 30° = 6*√3/2 = 3√3.
V1 = V(ABCNM) = (1/3)*21*3√3 = 21√3 куб.ед.
Площадь основания призмы So = 6²√3/4 = 9√3 кв.ед.
Объём призмы V = 9√3*8 = 72√3 куб.ед.
Объём отсечённой части призмы равен V2 = 72√3 - 21√3 = 51√3 куб.ед.
ОтношениеV1/V2 = 21√3/51√3 = 7/17.
Объяснение: