Предмет: Математика,
автор: Аноним
помогите с диф уравнениями
Приложения:
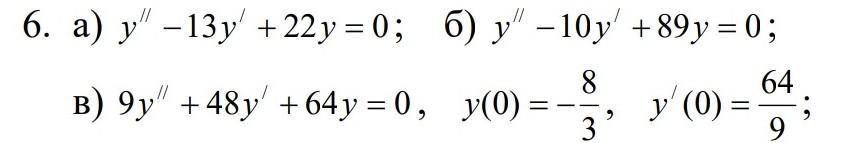
Ответы
Автор ответа:
0
Ответ:
везде замена:
а)
общее решение
б)
общее решение
в)
общее решение
частное решение
Похожие вопросы
Предмет: Русский язык,
автор: tarapanov03
Предмет: Английский язык,
автор: vetashedevrik
Предмет: Русский язык,
автор: Алина1719
Предмет: Математика,
автор: hdhfjdn
Предмет: Математика,
автор: Аноним