Предмет: Геометрия,
автор: gymapg
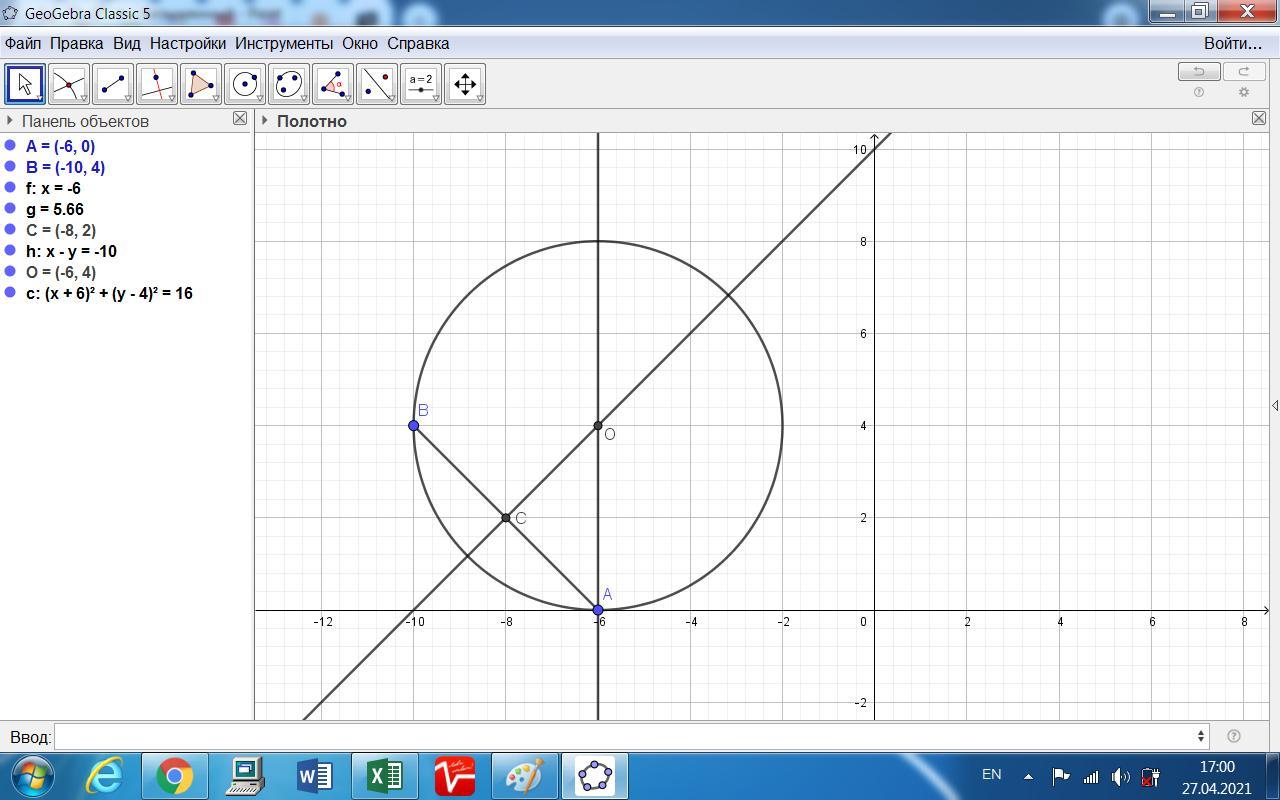
4.26. Найдите центр и радиус окружности, касающейся оси Ох в том
ке А(-6; 0) и проходящей через точку B(-10; 4).
Ответы
Автор ответа:
5
Центр окружности находится на пересечении двух перпендикуляров - один это радиус в точку касания, второй - к середине хорды АВ.
Вектор АВ: (-10-(-6); 4-0) = (-4; 4).
Угловой коэффициент равен к = 4/(-4) = -1.
Угловой коэффициент перпендикуляра к АВ равен к1 = -1/к = -1/-1 = 1.
Уравнение перпендикуляра у = х + в. Для определения слагаемого в надо подставить координаты точки, через которую проходит прямая.
Находим координаты середины АВ.
С((-10-6)/2; (4+0)/2) = (-8; 2).
Уравнение СО: у = х + в. Подставим точку С.
2 = -8 + в, отсюда в = 2 + 8 = 10.
Уравнение СО: у = х + 10.
Находим координаты центра при х = -6.
у = -6 + 10 = 4.
Ответ: центр(-6; 4), радиус равен 4.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: katia3443
Предмет: Английский язык,
автор: kris20061
Предмет: Русский язык,
автор: natalyatabert
Предмет: Английский язык,
автор: ГлупыйВаленок
Предмет: Алгебра,
автор: Аноним