Предмет: Геометрия,
автор: GennadijChuma3
Знайдіть кути правильного многокутника, центральний кут якого дорівнює 40 градусів. Скільки сторін має цей многокутник?
Ответы
Автор ответа:
8
Ответ:
α = 140°
n = 9 - количество сторон
Объяснение:
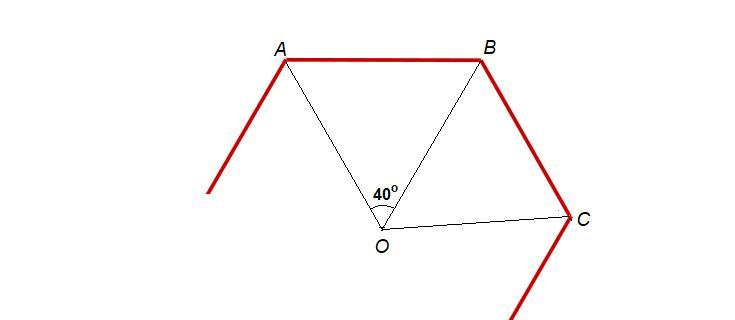
Если соединить центр правильного n-угольника с его вершинами, то получится n равных равнобедренных треугольников с углом при вершине 40°.
Сумма всех этих углов составляет 360° (полный угол). Тогда количество сторон многоугольника:
n = 360° : 40° = 9
Углы при основании одного такого треугольника:
∠ОАВ = ∠ОВА = (180° - 40°) : 2 = 140° : 2 = 70°
Тогда угол правильного многоугольника:
α = ∠ABC = 70° · 2 = 140°
Или можно найти внутренний угол правильного n-угольника по формуле:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ansarova01
Предмет: Русский язык,
автор: olgaivanova04
Предмет: Русский язык,
автор: liuda202nereti
Предмет: История,
автор: бвбв
Предмет: Математика,
автор: Анастасия9871