Question

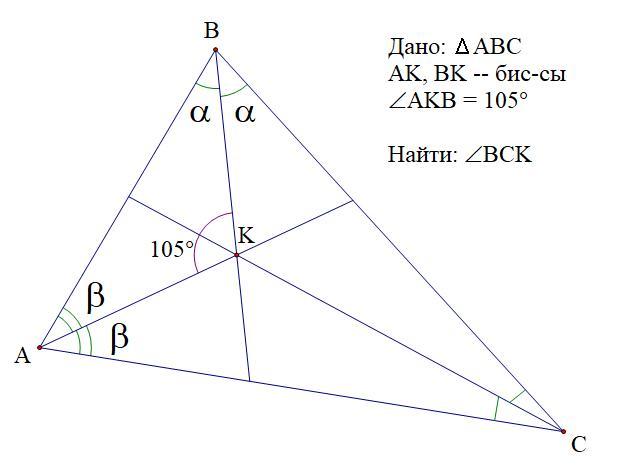
В треугольнике ABC пересекаются биссектрисы ∡A и ∡B. Точка пересечения K соединена с третьей вершиной C. Определи ∡BCK, если ∡AKB=105°.

Ответ: ∡BCK = °.
пожалуйста срочно

Answer 1

Ответ:

отрезок, соединяющий т.С и т.К - тоже биссектриса.

из треуг. АКВ a+b=180-105=75

из треуг. АВС С=180-(2a+2b)=180-2(a+b)=180-2*75=30

BCK=C/2=30/2= 15

Answer 2

Ответ: ∠BCK = 15°

Объяснение:

1. Пусть ∠ABK = α, ∠BAK = β, тогда ∠ABC = 2α, ∠BAC = 2β.

Рассмотрим ΔAKB:

По теореме о сумме углов треугольника имеем:

∠ABK + ∠BAK + ∠AKB = 180°

α + β + 105° = 180°

α + β = 75°

2. Рассмотрим ΔABС:

По теореме о сумме углов треугольника имеем:

∠ABC + ∠BAC + ∠ACB = 180°

2α + 2β + ∠ACB = 180°

∠ACB = 180° - 2(α + β)

∠ACB = 180° - 2 * 75°

∠ACB  = 30°

3. Биссектрисы треугольника пересекаются в одной точке.

Точка K -- точка пересечения биссектрис ⇒ CK -- биссектриса ∠ACB ⇒ ∠BCK = $\frac{1}{2}$∠ACB = $\frac{1}{2}$ * 30° = 15°