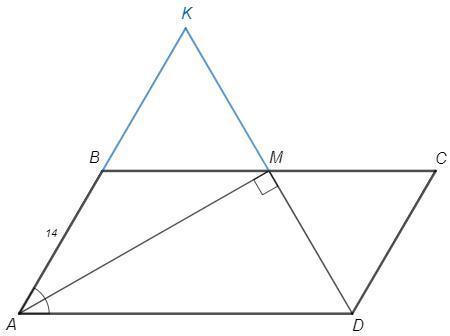
В параллелограмме ABCD биссектриса угла А, равного 60°, пересекает сторону ВС в точке М. Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB=14. Запишите решение и ответ.
Ответы
В параллелограмме ABCD биссектриса угла А, равного 60°, пересекает сторону ВС в точке М. Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB=14
Объяснение:
1) В параллелограмме ABCD, АМ- биссектриса ⇒∠ВАМ=∠DAM=30°.
И накрест лежащие углы равны при ВС║АD , АМ-секущая ⇒∠DAM=∠ВМС=30°. Значит ΔАВМ-равнобедренный и АВ=ВМ=14 (ед).
2) Развернутый угол ∠ВМС=∠ВАМ+∠АМD+∠СМD ⇒ ∠СМD=180°-90°-30°=60° .
Угол ∠ВСD=60° по свойству противоположных углов параллелограмма. Тогда в ΔМСD угол ∠МDC=180°-2*60°=60° ⇒
ΔМСD- равносторонний и МС=СD=DM=14( ед).
3) ВС=ВМ+МС=14+14=28 (ед)
Р=2(АВ+ВС)=2*(14+28)=84( ед).

Пусть AB и DM пересекаются в точке K
AM - биссектриса и высота => △KAD - равнобедренный, AM - медиана
BM||AD, KM=MD => KB=AB (т Фалеса)
AD =AK =2AB
P(ABCD) =2(AB+AD) =6AB =14*6 =84 (см)