Question

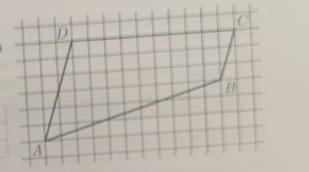
на клетчатой бумаге с размером 1×1 изображена трапеция ABCD. Во сколько раз основание BC меньше высоты трапеции?​

Answer 1

Основание ВС найдем из прямоугольного Δ с катетами 1 и 3 клетки, где ВС является гипотенузой:  ВС² = 1² + 3² = 10 ⇒ ВС = √10, аналогично из прямоугольного Δ с катетами 2 и 6 отыщем основание AD:

2² + 6² = AD² ⇒ AD² = 40 ⇒ AD = √40 = 2√10. Площадь ABCD (вычитаем

из площади прямоугольника, целиком захватывающего трапецию, площади фигур, которые образованы сторонами этой трапеции) равна

12·6 - (0,5·2·6 + 0,5·3·1 + 3·1 + 0,5·3·11) = 72 - (6+1,5+3+16,5) = 72 - 27 = 45.

В то же время S(ABCD) = h·(√10 + 2√10)/2 = 45, (h - высота трапеции) ⇒

h = 90/(√10 + 2√10) = 90/(3√10), h/ВС = 90/(3√10) : √10 = 30/(√10²) = 30/10 = = 3. Ответ: основание ВС меньше высоты трапеции в 3 раза