Question

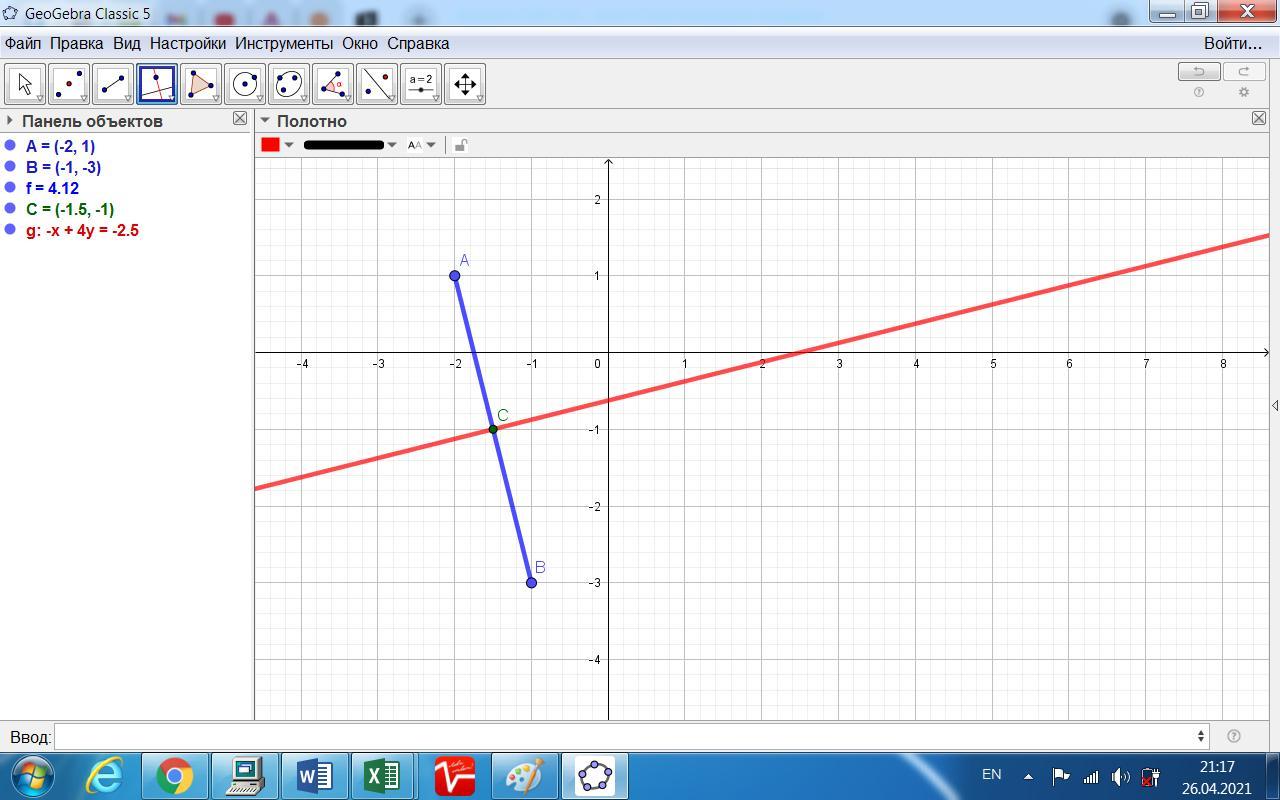
2. Составить уравнение линии, все точки которой оинаково удалены от точек
А(-2; 1) и B(-1 -3)

Answer 1

Даны точки А(-2; 1) и B(-1 -3).

Линия, все точки которой одинаково удалены от двух заданных точек А и В, - это перпендикуляр к середине отрезка АВ.

Вектор АВ: (-1-(-2); -3-1) = (1; -4).

Находим координаты середины АВ.

С = (А(-2; 1) + B(-1 -3)) / 2 = (-1,5; -1).

Угловой коэффициент прямой АВ равен: к = -4/1 = -4.

Для перпендикулярной прямой угловой коэффициент равен к(1) = -1/к.

к(1) = -1/-4 = 1/4.

Тогда уравнение имеет вид у = (1/4)х + в.

Для определения слагаемого "в" подставим в уравнение координаты точки С: -1 = (1/4)*(-1,5) + в, отсюда в = -1 + 3/8 = -5/8.

Ответ: уравнение заданной линии -

у = (1/4)х - (5/8) или в общем виде 2х - 8у - 5 = 0.