Предмет: Геометрия,
автор: Nastya666053395
Окружность, вписанная в треугольник АВС, периметр которого равен 56см. Точка касания окружности со стороной АВ делит эту сторону в отношении 3:2, Считая от вершины А. Точка касания со стороной ВС удалена от вершины С на 8см. Найдите стороны треугольника.
Ответы
Автор ответа:
0
Ответ:
20 см, 16 см, 20 см.
Объяснение:
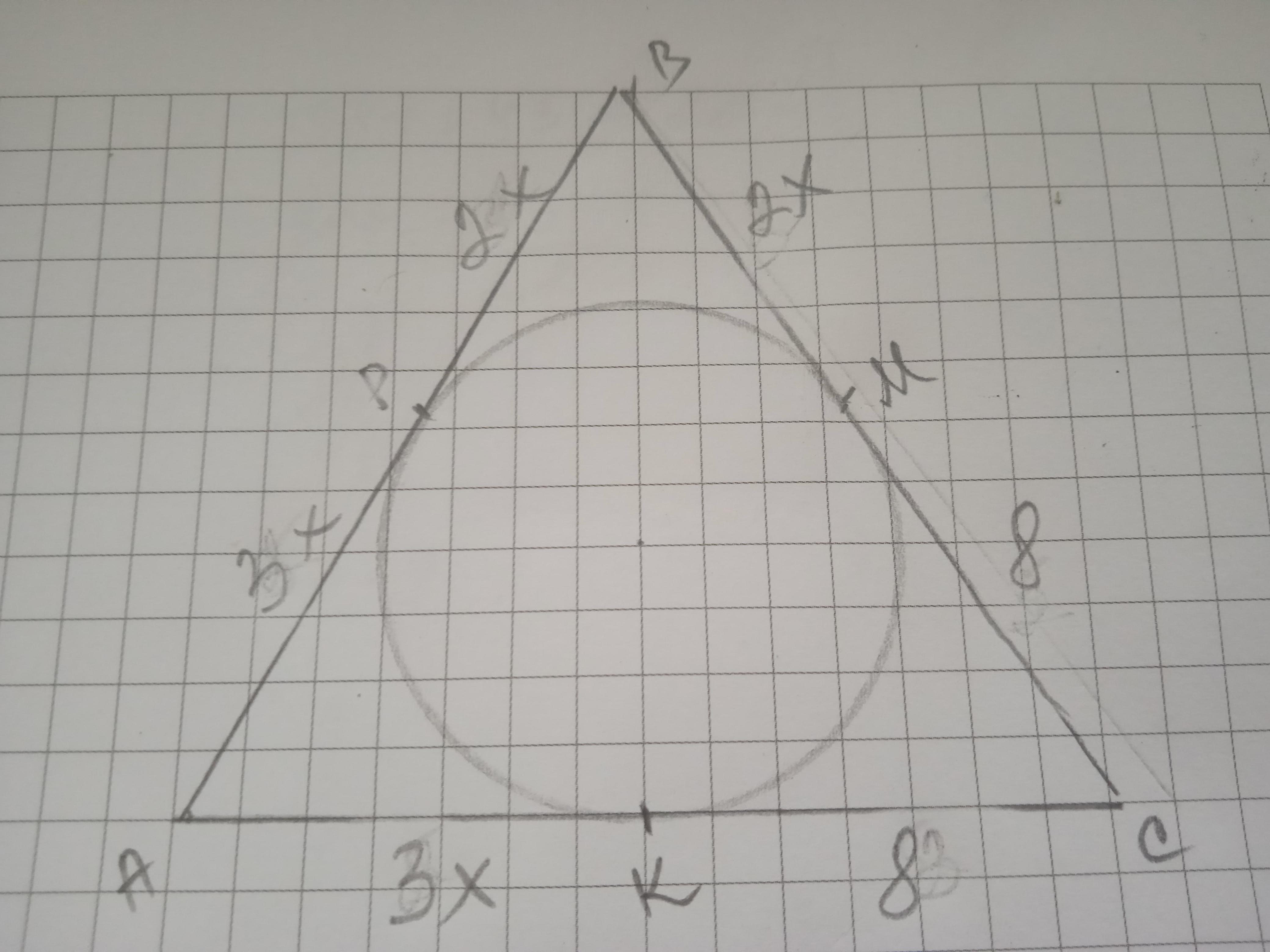
Имеем ΔАВС, где АВ, ВС, АС - касательные к окружности. Известно, что отрезки касательных, проведенных к окружности из одной точки, равны между собой. Тогда по условию:
АР=АК=3х см
ВР=ВМ=2х см, СМ=СК=8 см
Составим уравнение:
3х+3х+2х+2х+8+8=56
10х=40
х=4
АВ=3*4+2*4=20 см
ВС=2*4+8=16 см
АС=3*4+8=20 см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: geydar2002
Предмет: Немецкий язык,
автор: roma092
Предмет: Русский язык,
автор: mrazrashoev
Предмет: География,
автор: Ангелиночка1131
Предмет: Русский язык,
автор: Skvaler