Предмет: Математика,
автор: kusalisa35
На оценку 5
1 вариант, второй пример
Приложения:
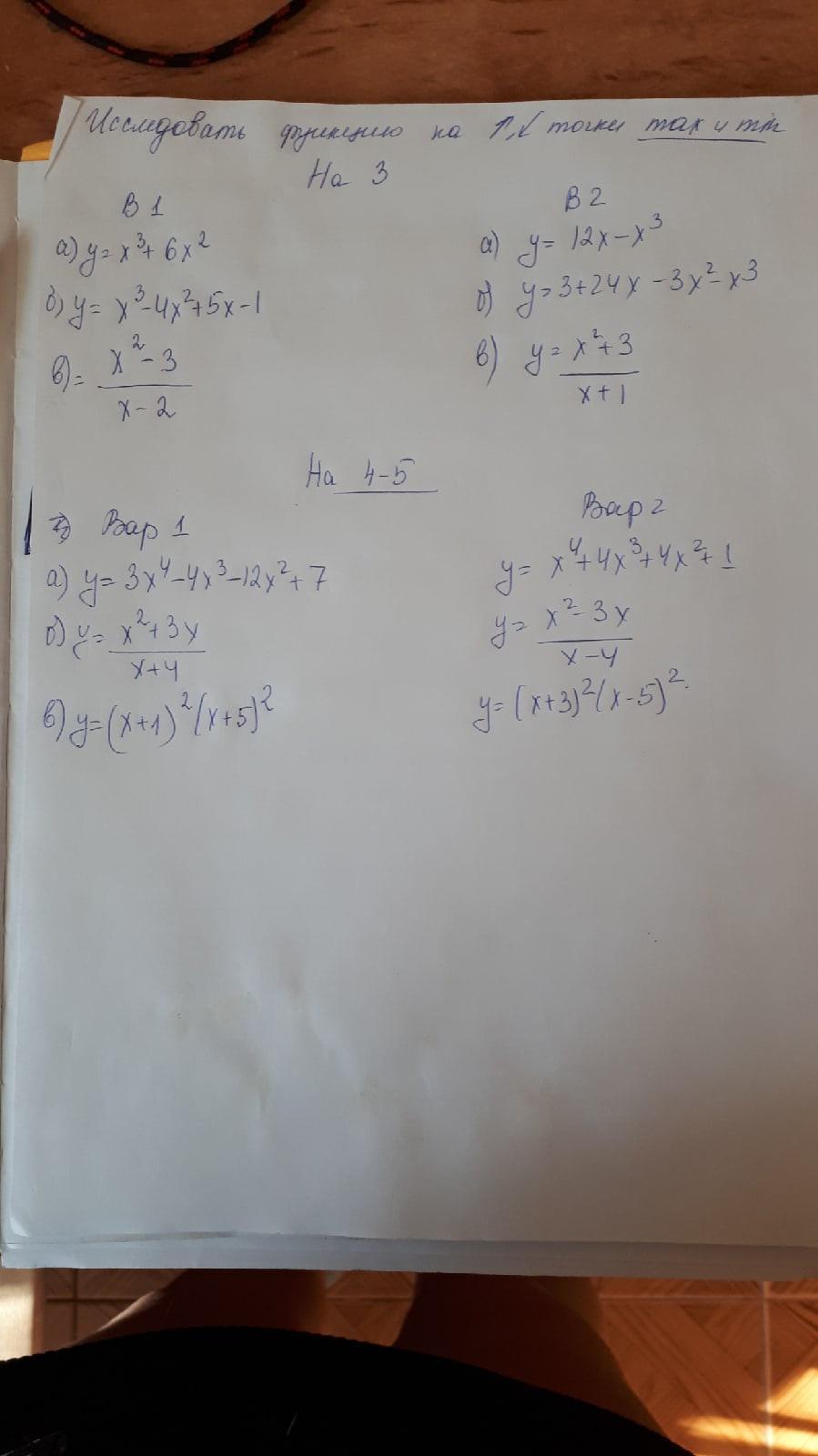
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
находим производную
f'(x) =0
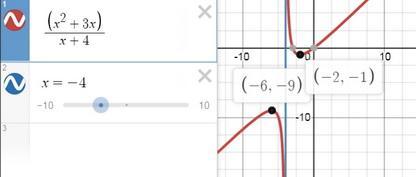
x² +8x +12 = 0 ⇒ x1 =-2; x2 = -6 - критические точки
ОДЗ х≠ -4 (х= -4 - вертикальная асимптота)
у нас два промежутка, где определена функция (-∞; -4) и (-4; +∞)
теперь посмотрим какая точка есть минимум а какая максимум
вторая производная (не буду заморачиваться расчетом, там все просто f''(x) = (f'(x))' )
f''(x)= 8/(x+4)³
промежуток
(-∞; -4) f'' (-6) = -1 < 0, тогда f(-6) = -9 локальный максимум
промежуток
(-4; +∞) f''(-2) = 1 > 0, тогда f(-2) = -1 локальный минимум
Приложения:
Похожие вопросы
Предмет: Французский язык,
автор: Аноним
Предмет: Русский язык,
автор: анютакрута
Предмет: Английский язык,
автор: larisapak200009
Предмет: Математика,
автор: 228500
Предмет: История,
автор: giftik