Предмет: Алгебра,
автор: sabina03199
Рациональное неравенство. Урок 6
Найди наибольшее целое значение, удовлетворяющее неравенству
1/х +1/4 <= 0
≤ 0, и отметь его на координатной прямой.
Ответ
Ответы
Автор ответа:
2
Ответ:
- 1.
Объяснение:
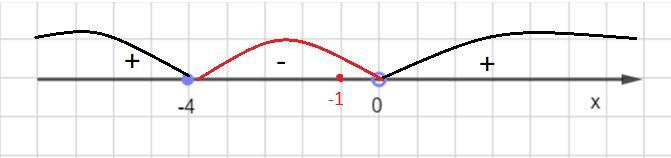
Решим данное неравенство методом интервалов. Отметим на числовой прямой точки - 4 и 0 . Точка -4 включена, а точку 0 надо исключить, так как на нуль делить нельзя. Определим знак на каждом полученном промежутке и получим
x∈ [-4 ; 0)
Наибольшее целое решение неравенства -1.
Число - 1 показано на числовой прямой.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: ilia021105
Предмет: Українська мова,
автор: olgakoval2001r
Предмет: Русский язык,
автор: elenashilova777
Предмет: Математика,
автор: kirill009007
Предмет: Алгебра,
автор: RedBeast12