Question

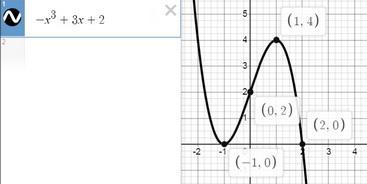
Исследовать функцию f(x)=-x^3+3x+2 с помощью производной и построить график

Answer 1

Ответ:

Пошаговое объяснение:

с помощью производной мы можем найти

1) экстремумы

2) промежутки возрастания и убывания

3) выпуклость/вогнутость

все остальные тсследования производятся без производных. из них я только найду нули и точку пересечения с оу - для удобства построения графика

итак.

нули -x³+3x+2 = 0  ⇒ x1 = 2;  x2 = -1

пересечение с осью оу   х = 0;   у= 2

теперь производная

f'(x) = (-x³+3x+2)' = -3x² +3 = 3(1-x²)

1) экстремумы

3(1-x²) = 0   x1 = -1   x2 = 1 - это критические точки

f(-1) = 0 - локальный минимум

f(1) = 4 - локальный маскимум

2) интервалы возрастания / убывания

мы имеем три интервала. посмотрим знаки производной на каждом

(-∞ ;-1)   f'(x) < 0  функция убывает

(-1; 1)      f'(x) > 0 функция возрастает

(1; +∞)    f'(x) < 0  функция убывает

3) выпуклость /вогнутость

вторая производная

f''(x) = -6x

-6х =0     ⇒  х1 = 0   точка перегиба

(-∞ ;0)   f''(x) > 0 функция вогнута

(0; +∞)   f''(x) < 0 функция выпукла